
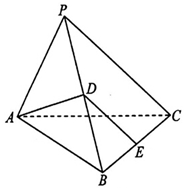
 在三棱锥P-ABC中,AP=AB,平面PAB⊥平面ABC,∠ABC=90°,D,E分别为PB,BC的中点.
在三棱锥P-ABC中,AP=AB,平面PAB⊥平面ABC,∠ABC=90°,D,E分别为PB,BC的中点.分析 (1)推导出DE∥PC,由此能证明DE∥平面PAC.
(2)推导出AD⊥PB,BC⊥AB,从而AD⊥BC,进而AD⊥平面PBC,由此能证明DE⊥AD.
解答 证明:(1)因为D,E分别为PB,BC的中点,
所以DE∥PC,…(2分)
又DE?平面PAC,PC?平面PAC,
故DE∥平面PAC.…(5分)
(2)因为AP=AB,PD=DB,所以AD⊥PB,…(7分)
因为平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,
又BC⊥AB,BC?平面ABC,所以BC⊥平面PAB,…(10分)
因为AD?平面PAB,所以AD⊥BC,…(11分)
又PB∩BC=B,PB,BC?平面ABC,故AD⊥平面PBC,…(13分)
因为DE?平面PBC,所以DE⊥AD.…(14分)
点评 本题考查线面平行、线线垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
 一个四面体的顶点都在球面上,它们的正视图、侧视图、俯视图都是如图.图中圆内有一个以圆心为中心边长为2的正方形.则这个四面体的外接球的表面积是( )
一个四面体的顶点都在球面上,它们的正视图、侧视图、俯视图都是如图.图中圆内有一个以圆心为中心边长为2的正方形.则这个四面体的外接球的表面积是( )| A. | 3π | B. | 4π | C. | 12π | D. | 14π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数f(x)的图象经过(0,0)点 | B. | y=|x+1|+|x-1|(x∈(-4,4])是偶函数 | ||
| C. | 幂函数y=x${\;}^{\frac{1}{2}}$过(1,1)点 | D. | y=sin2x(x∈[0,5π])是以π为周期的函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com