
(理)命题“若两个正实数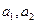 满足
满足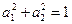 ,那么
,那么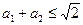 。”
。”
证明如下:构造函数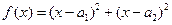 ,因为对一切实数
,因为对一切实数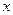 ,恒有
,恒有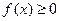 ,
,
又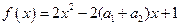 ,从而得
,从而得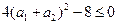 ,所以
,所以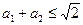 。
。
根据上述证明方法,若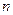 个正实数满足
个正实数满足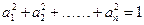 时,你可以构造函数
时,你可以构造函数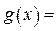 _______ ,进一步能得到的结论为 ______________ (不必证明).
_______ ,进一步能得到的结论为 ______________ (不必证明).
 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com