
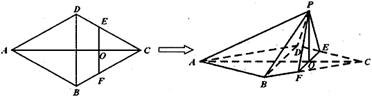
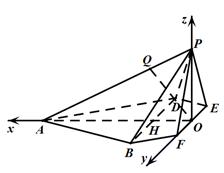
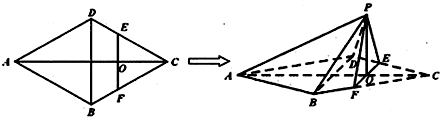
如图,在边长为4的菱形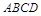 中,
中,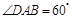 .点
.点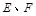 分别在边
分别在边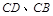 上,点
上,点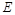 与点
与点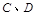 不重合,
不重合,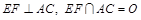 .沿
.沿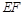 将
将 翻折到
翻折到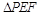 的位置,使平面
的位置,使平面 平面
平面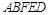 .
.
(1)求证: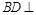 平面
平面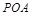 ;
;
(2)设点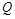 满足
满足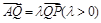 ,试探究:当
,试探究:当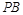 取得最小值时,直线
取得最小值时,直线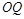 与平面
与平面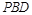 所成角的大小是否一定大于
所成角的大小是否一定大于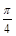 ?并说明理由.
?并说明理由.
(1)证明:∵ 菱形 的对角线互相垂直,∴
的对角线互相垂直,∴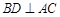 ,∴
,∴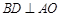 ,
,
∵ 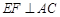 ,∴
,∴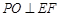 .
.
∵ 平面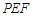 ⊥平面
⊥平面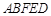 ,平面
,平面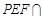 平面
平面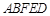
 ,且
,且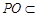 平面
平面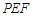 ,
,
∴ 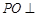 平面
平面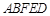 , ∵
, ∵ 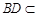 平面
平面 ,∴
,∴ 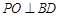 ……………4分
……………4分
(2)如图,以 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系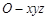 .
.
设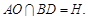 因为
因为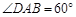 ,所以
,所以 为等边三角形,
为等边三角形,
故 ,
,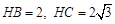 .又设
.又设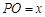 ,则
,则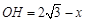 ,
,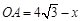 .
.
所以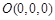 ,
,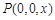 ,
,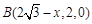 ,
,
故
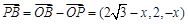 ,
,
所以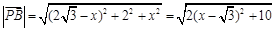 ,
,
当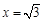 时,
时,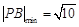 .此时
.此时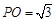 ,………………………………6分
,………………………………6分
设点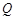 的坐标为
的坐标为 ,由(1)知,
,由(1)知,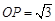 ,则
,则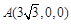 ,
,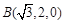 ,
,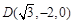 ,
,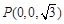 .所以
.所以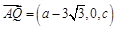 ,
,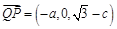 ,
,
∵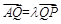 , ∴
, ∴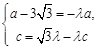
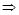 .
.
∴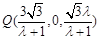 ,∴
,∴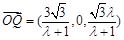 . 10分
. 10分
设平面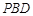 的法向量为
的法向量为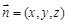 ,则
,则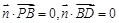 .
.
∵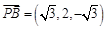 ,
,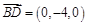 ,∴
,∴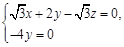
取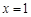 ,解得:
,解得: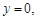
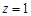 ,
所以
,
所以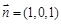 .……………………………… 8分
.……………………………… 8分
设直线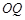 与平面
与平面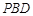 所成的角
所成的角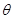 ,
,
∴
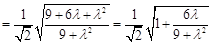 .………………………………………………
10分
.………………………………………………
10分
又∵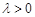 ∴
∴ .
∵
.
∵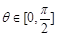 ,∴
,∴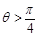 .
.
因此直线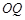 与平面
与平面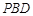 所成的角大于
所成的角大于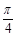 ,即结论成立
,即结论成立
【解析】略


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
| V1 |
| V2 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山西省高三1月月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
如图,在边长为4的菱形 中,
中, .点
.点 分别在边
分别在边 上,点
上,点 与点
与点 不重合,
不重合, ,
, .沿
.沿 将
将 翻折到
翻折到 的位置,使平面
的位置,使平面 ⊥平面
⊥平面 .
.

(1)求证: ⊥平面
⊥平面 ;
;
(2)当 取得最小值时,请解答以下问题:
取得最小值时,请解答以下问题:
(i)求四棱锥 的体积;
的体积;
(ii)若点 满足
满足 =
=
 (
( ),试探究:直线
),试探究:直线 与平面
与平面 所成角的大小是否一定大于
所成角的大小是否一定大于 ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
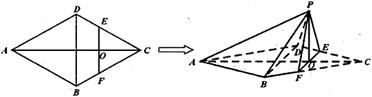
如图,在边长为4的菱形![]() 中,
中,![]() .点
.点![]() 分别在边
分别在边![]() 上,点
上,点![]() 与点
与点![]() 不重合,
不重合,![]() .沿
.沿![]() 将
将![]() 翻折到
翻折到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)设点![]() 满足
满足![]() ,试探究:当
,试探究:当![]() 取得最小值时,直线
取得最小值时,直线![]() 与平面
与平面![]() 所成角的大小是否一定大于
所成角的大小是否一定大于![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com