
如图所示,在半径为1的⊙O中,引两条互相垂直的直径AE和BF,在EF上取点C,弦AC交BF于P,弦CB交AE于Q,弦EF交AC于D.
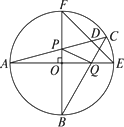
证明:四边形APQB的面积是1.
|
证明:因为AE、BF为互相垂直的两条直径,垂足O为圆心, 所以AE、BF互相平分,垂直且相等, 所以四边形ABEF是正方形. 所以∠ACB=∠AEF=45°,即∠DCQ=∠QED. 所以D、Q、E、C四点共圆. 连结CE、DQ, 则∠DCE+∠DQE=180°. 因为AE为⊙O的直径, 所以∠DCE=90°,∠DQE=90°. 因为∠FOE=90°, 进而DQ∥BF, 所以S△BPQ=S△BPD. 所以S△ABP+S△BPQ=S△ABP+S△BPD, 即S四边形ABQP=S△ABD. 因为⊙O的半径为1, 所以正方形边长为2, 即AB=AF=2. 所以S四边形ABQP=S△ABD= 分析:由已知条件可以证明四边形ABEF是正方形,且边长为 |


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源:2012年人教A版高中数学必修三3.3几何概型练习卷(二)(解析版) 题型:填空题
如图所示,在半径为1的半圆内放置一个边长为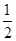 的正方形ABCD,向半圆内任投一点,则点落在正方形内的概率为________.
的正方形ABCD,向半圆内任投一点,则点落在正方形内的概率为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com