
 ��ͼ����֪�뾶Ϊ1�ġ�O1��x�ύ��A��B���㣬OMΪ��O1�����ߣ��е�ΪM����M�ڵ�һ���ޣ�Բ��O1������Ϊ��2��0�������κ���y=-x2+bx+c��ͼ��A��B���㣮
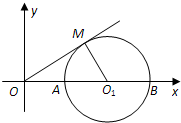
��ͼ����֪�뾶Ϊ1�ġ�O1��x�ύ��A��B���㣬OMΪ��O1�����ߣ��е�ΪM����M�ڵ�һ���ޣ�Բ��O1������Ϊ��2��0�������κ���y=-x2+bx+c��ͼ��A��B���㣮
|
|
| |2k| | ||
|
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
|
|
| ||
| 3 |
|
|
| 3 |
| 4 |
| ||
| 4 |
| ||
| 3 |
| 3 |
| 4 |
| ||
| 4 |


 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�

| x2 |
| a2 |
| y2 |
| b2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
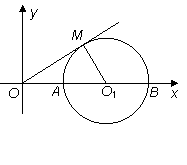
��ͼ����֪�뾶Ϊ1�ġ�O1��![]() �ύ��
�ύ��![]() ���㣬
���㣬![]() Ϊ��O1�����ߣ��е�Ϊ
Ϊ��O1�����ߣ��е�Ϊ![]() ����
����![]() �ڵ�һ���ޣ�Բ��
�ڵ�һ���ޣ�Բ��![]() ������Ϊ
������Ϊ![]() �����κ���
�����κ���![]() ��ͼ��
��ͼ��![]() ���㣮
���㣮
��1������κ����Ľ���ʽ��
��2��������![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��3���߶�![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ����
��ʹ����![]() Ϊ�������������
Ϊ�������������![]() ���ƣ������ڣ���������з��������ĵ�
���ƣ������ڣ���������з��������ĵ�![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011���Ϻ��������߿���ѧ��ģ�Ծ��������Ͼ����������棩 ���ͣ������
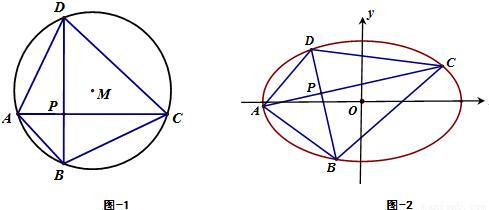
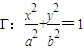 ��a��b��0�����ڽ��ı���ABCD�ĶԽ���AC��BD���ֱ�ҽ��ڵ�P�������һ������Ȼ�õIJ��룬�����Ը���֤��������
��a��b��0�����ڽ��ı���ABCD�ĶԽ���AC��BD���ֱ�ҽ��ڵ�P�������һ������Ȼ�õIJ��룬�����Ը���֤���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011���Ϻ����������߿���ѧ��ģ�Ծ��������Ͼ����������棩 ���ͣ������
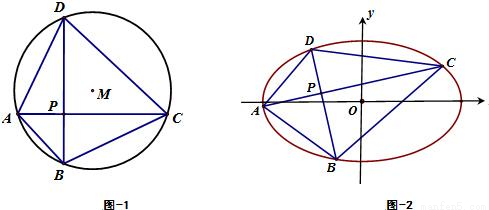
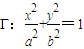 ��a��b��0�����ڽ��ı���ABCD�ĶԽ���AC��BD���ֱ�ҽ��ڵ�P�������һ������Ȼ�õIJ��룬�����Ը���֤��������
��a��b��0�����ڽ��ı���ABCD�ĶԽ���AC��BD���ֱ�ҽ��ڵ�P�������һ������Ȼ�õIJ��룬�����Ը���֤���������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com