
如图,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.
(1)若=,求证:无论点P在D1D上如何移动,总有BP⊥MN;
(2)若D1P:PD=1∶2,且PB⊥平面B1MN,求二面角M-B1N-B的余弦值;
(3)棱DD1上是否总存在这样的点P,使得平面APC1⊥平面ACC1?证明你的结论.
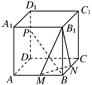
(1)证明:连结AC、BD,则BD⊥AC,
∵=,
∴MN∥AC,∴BD⊥MN.
又∵DD1⊥平面ABCD,
∴DD1⊥MN,
∵BD∩DD1=D,∴MN⊥平面BDD1.
又P无论在DD1上如何移动,总有BP⊂平面BDD1,
∴无论点P在D1D上如何移动,总有BP⊥MN.
(2)以D为坐标原点,DA、DC、DD1所在直线分别为x轴、y轴、z轴,建立如图所示的坐标系.设正方体的棱长为1,AM=NC=t,
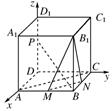
则M(1,t,0),N(t,1,0),B1(1,1,1),
P(0,0,),B(1,1,0),A(1,0,0),
∵=(0,1-t,1),
B=
又∵BP⊥平面MNB1,
∴·B=0,
即t-1+=0,∴t=,
∴=(0,,1),
M=(-,,0).
设平面MNB1的法向量n=(x,y,z),
由,
得x=y,z=-y.
令y=3,则n=(3,3,-2).
∵AB⊥平面BB1N,
∴A是平面BB1N的一个法向量,A=(0,1,0).
设二面角M-B1N-B的大小为θ,
∴cos〈n,A〉
=
=.
则二面角M-B1N-B的余弦值为.
(3)存在点P,且P为DD1的中点,
使得平面APC1⊥平面ACC1.
证明:∵BD⊥AC,BD⊥CC1,
∴BD⊥平面ACC1.
取BD1的中点E,连PE,
则PE∥BD,
∴PE⊥平面ACC1.
∵PE⊂平面APC1,
∴平面APC1⊥平面ACC1.
【解析】略


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 现有一块棱长为a的正方体形的木料,如图,M、N、P分别为AD、CD、BB1的中点.现要沿过M、N、P三点的平面将木料锯开.
现有一块棱长为a的正方体形的木料,如图,M、N、P分别为AD、CD、BB1的中点.现要沿过M、N、P三点的平面将木料锯开.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,M、N、P分别为空间四边形ABCD的边AB,BC,CD上的点,且AM:MB=CN:NB=CP:PD.
如图,M、N、P分别为空间四边形ABCD的边AB,BC,CD上的点,且AM:MB=CN:NB=CP:PD.查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省唐山一中高二(上)期中数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省唐山一中高二(上)期中数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省上饶市重点中学高三第二次联考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com