
| A. | 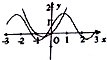 | B. | 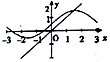 | C. |  | D. | 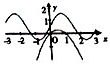 |
分析 分别令a=0,a=1,a>1,a<0.根据二次函数(或一次函数,常数函数)和三角函数的图象和性质判断即可.
解答 解:当a=1时,函数y=sinx+$\frac{1}{2}$与函数y=x,图象B符合,
当a=0时,函数y=$\frac{1}{2}$与函数y=x2+x,图象C符合,
当a>1时,y=(a-1)x2+x开口向上,对称轴x=-$\frac{1}{2(a-1)}$<0,y=sinax+$\frac{1}{2}$的图象在y=sinax的基础上向上平移$\frac{1}{2}$单位,图象A符合,
当a<0时,y=(a-1)x2+x开口向下,对称轴x=-$\frac{1}{2(a-1)}$>0,y=sinax+$\frac{1}{2}$的图象在y=sin|a|x的基础上翻转180后,再向上平移$\frac{1}{2}$单位,图象D不符合,
故选:D.
点评 本题考查了图象和识别,以及二次函数和三角函数的图象和性质,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | y=±2x | B. | y=±x | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
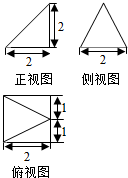 已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体得体积是( )cm2.
已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体得体积是( )cm2.| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 3 | D. | 0或3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q是真命题 | B. | p∨q是真命题 | C. | ¬p是真命题 | D. | ¬q是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com