
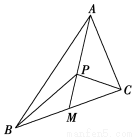
在△ABC中,中线长AM=2.
(1)若 =-2
=-2 ,求证:
,求证: +
+ +
+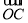 =0;
=0;
(2)若P为中线AM上的一个动点,求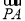 ·(
·(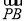 +
+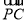 )的最小值.
)的最小值.
(1)见解析;(2)最小值-2.
【解析】
试题分析:(1) ∵M是BC的中点,∴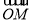 =
= (
( +
+ ).代入
).代入 =-2
=-2 ,得
,得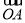 =-
=- -
- ,即
,即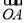 +
+ +
+ =0
=0
(2) 若P为中线AM上的一个动点,若AM=2,我们易将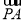 ·(
·( +
+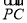 ),转化为-2|
),转化为-2|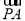 ||
|| |=2(x-1)2-2的形式,然后根据二次函数在定区间上的最值的求法,得到答案.
|=2(x-1)2-2的形式,然后根据二次函数在定区间上的最值的求法,得到答案.
试题解析:(1)证明:∵M是BC的中点,
∴ =
=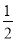 (
(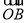 +
+ ) ..3分
) ..3分
代入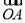 =-2
=-2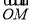 ,得
,得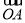 =-
=-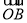 -
- , .2分
, .2分
即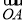 +
+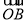 +
+ =0 1分
=0 1分
(2)设| |=x,则|
|=x,则|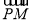 |=2-x(0≤x≤2) .1分
|=2-x(0≤x≤2) .1分
∵M是BC的中点,∴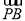 +
+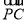 =2
=2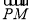 2分
2分
∴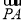 ·(
·(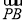 +
+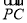 )=2
)=2 ·
· =-2|
=-2|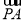 ||
|| |
|
=-2x(2-x)=2(x2-2x)=2(x-1)2-2, 2分
当x=1时,取最小值-2 ..1分
考点:平面向量数量积的运算.


科目:高中数学 来源:2016届辽宁省抚顺市六校联合体高一下学期期末考试数学试卷(解析版) 题型:选择题
已知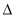 ABC和点M满足
ABC和点M满足 ,若存在实数
,若存在实数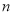 使得
使得 成立,则
成立,则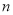 = ( )
= ( )
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:高中数学 来源:2016届辽宁东北育才学校等三校高一下学期期末联考数学试卷(解析版) 题型:选择题
已知MP,OM,AT分别为角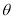
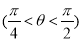 的正弦线、余弦线、正切线,则一定有( )
的正弦线、余弦线、正切线,则一定有( )
A.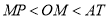 B.
B.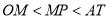
C. D.
D.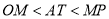
查看答案和解析>>
科目:高中数学 来源:2016届贵州省高一下学期期中考试数学试卷(解析版) 题型:填空题
在平行四边形ABCD中,E和F分别是边CD和BC的中点.若 =λ
=λ +μ
+μ ,其中λ,μ∈R,则λ+μ=__________.
,其中λ,μ∈R,则λ+μ=__________.
查看答案和解析>>
科目:高中数学 来源:2016届福建省福州市高一下学期期末联考数学试卷(解析版) 题型:填空题
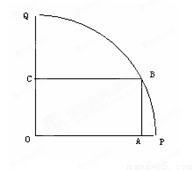
如图,在半径为2,中心角为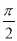 的扇形的内接矩形OABC(只有B在弧上)的面积的最大值= .
的扇形的内接矩形OABC(只有B在弧上)的面积的最大值= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com