
下列命题正确的个数是( )
①“在三角形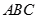 中,若
中,若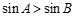 ,则
,则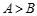 ”的否命题是真命题;
”的否命题是真命题;
②命题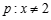 或
或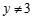 ,命题
,命题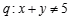 则
则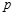 是
是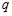 的必要不充分条件;
的必要不充分条件;
③“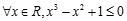 ”的否定是“
”的否定是“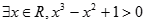 ”.
”.
| A.0 | B.1 | C.2 | D.3 |
D
解析试题分析:①该命题的否命题是:在三角形ABC中,若sinA≤sinB,则A≤B;若A,B∈(0, ],∵正弦函数y=sinx在(0,
],∵正弦函数y=sinx在(0, ]上是增函数,∴sinA≤sinB可得到A≤B;若A∈(0,
]上是增函数,∴sinA≤sinB可得到A≤B;若A∈(0, ],B∈(
],B∈( ,π),sinA<sinB能得到A<B;若A∈(
,π),sinA<sinB能得到A<B;若A∈( ,π),B∈(0,
,π),B∈(0, ],则由sinA≤sinB,得到sin(π-A)≤sinB,∴π≤A+B,显然这种情况不存在;综上可得sinA≤sinB能得到A≤B,所以该命题正确;②由x≠2,或y≠3,得不到x+y≠5,比如x=1,y=4,x+y=5,∴p不是q的充分条件;若x+y≠5,则一定有x≠2且y≠3,即能得到x≠2,或y≠3,∴p是q的必要条件;∴p是q的必要不充分条件,所以该命题正确;③根据全称命题的否定是特称命题知道该命题正确;所以命题正确的个数为3.故选:D.
],则由sinA≤sinB,得到sin(π-A)≤sinB,∴π≤A+B,显然这种情况不存在;综上可得sinA≤sinB能得到A≤B,所以该命题正确;②由x≠2,或y≠3,得不到x+y≠5,比如x=1,y=4,x+y=5,∴p不是q的充分条件;若x+y≠5,则一定有x≠2且y≠3,即能得到x≠2,或y≠3,∴p是q的必要条件;∴p是q的必要不充分条件,所以该命题正确;③根据全称命题的否定是特称命题知道该命题正确;所以命题正确的个数为3.故选:D.
考点:1.四种命题;2.命题的否定.


科目:高中数学 来源: 题型:单选题
在给出如下四个命题:①若“ 且
且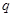 ”为假命题,则
”为假命题,则 、
、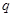 均为假命题;②命题“若
均为假命题;②命题“若 ,则
,则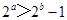 ”的否命题为“若
”的否命题为“若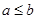 ,则
,则 ”;③“
”;③“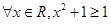 ”的否定是“
”的否定是“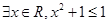 ”;④在
”;④在 中,“
中,“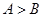 ”是“
”是“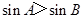 ”的充要条件.其中不正确的命题的个数是( )
”的充要条件.其中不正确的命题的个数是( )
| A.4 | B.3 | C.2 | D.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知函数f( +1)=x+1,则函数f(x)的解析式为( )
+1)=x+1,则函数f(x)的解析式为( )
| A.f(x)=x2 | B.f(x) =x2+1(x≥1) |
| C.f(x)=x2-2x+2 (x≥1) | D.f(x)=x2-2x(x≥1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com