
设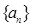 是各项为正数的无穷数列,
是各项为正数的无穷数列,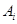 是边长为
是边长为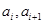 的矩形面积(
的矩形面积(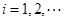 ),则
),则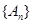 为等比数列的充要条件为
为等比数列的充要条件为
A.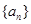 是等比数列。
是等比数列。
B.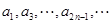 或
或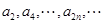 是等比数列。
是等比数列。
C.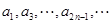 和
和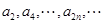 均是等比数列。
均是等比数列。
D.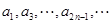 和
和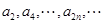 均是等比数列,且公比相同。
均是等比数列,且公比相同。
D
【解析】
试题分析:依题意可知Ai=ai?ai+1,
∴Ai+1=ai+1?ai+2,
若{An}为等比数列则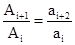 =q(q为常数),则a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比均为q;
=q(q为常数),则a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比均为q;
反之要想{An}为等比数列则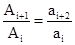 需为常数,即需要a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比相等;
需为常数,即需要a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比相等;
故{An}为等比数列的充要条件是a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比相同.
故选D
考点:本题主要考查充要条件的概念,等比数列的概念。
点评:此类问题,要既考查充分性,又要考查必要性,已作出准确判断。


 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源:2011年上海市招生考试理科数学 题型:选择题
设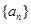 是各项为正数的无穷数列,
是各项为正数的无穷数列,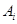 是边长为
是边长为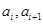 的矩形面积(
的矩形面积(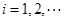 ),则
),则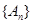 为等比数列的充要条件为〖答〗( )
为等比数列的充要条件为〖答〗( )
A 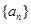 是等比数列。
是等比数列。
B 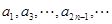 或
或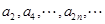 是等比数列。
是等比数列。
C 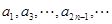 和
和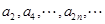 均是等比数列。
均是等比数列。
D 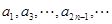 和
和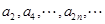 均是等比数列,且公比相同。
均是等比数列,且公比相同。
查看答案和解析>>
科目:高中数学 来源: 题型:
设![]() 是各项为正数的无穷数列,
是各项为正数的无穷数列,![]() 是边长为
是边长为![]() 的矩形面积(
的矩形面积(![]() ),则
),则![]() 为等比数列的充要条件为 ( )
为等比数列的充要条件为 ( )
A.![]() 是等比数列。
是等比数列。
B.![]() 或
或![]() 是等比数列。
是等比数列。
C.![]() 和
和![]() 均是等比数列。
均是等比数列。
D.![]() 和
和![]() 均是等比数列,且公比相同。
均是等比数列,且公比相同。
查看答案和解析>>
科目:高中数学 来源: 题型:
设![]() 是各项为正数的无穷数列,
是各项为正数的无穷数列,![]() 是边长为
是边长为![]() 的矩形面积(
的矩形面积(![]() ),则
),则![]() 为等比数列的充要条件为〖答〗 ( )
为等比数列的充要条件为〖答〗 ( )
A.![]() 是等比数列。
是等比数列。
B.![]() 或
或![]() 是等比数列。
是等比数列。
C.![]() 和
和![]() 均是等比数列。
均是等比数列。
D.![]() 和
和![]() 均是等比数列,且公比相同。
均是等比数列,且公比相同。
查看答案和解析>>
科目:高中数学 来源:2012届江西省上高二中高三第一次月考试卷理科数学 题型:单选题
设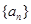 是各项为正数的无穷数列,
是各项为正数的无穷数列,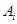 是边长为
是边长为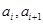 的矩形面积(
的矩形面积(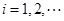 ),则
),则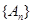 为等比数列的充要条件为( )
为等比数列的充要条件为( )
A.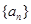 是等比数列。 是等比数列。 |
B.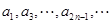 或 或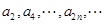 是等比数列。 是等比数列。 |
C.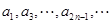 和 和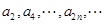 均是等比数列。 均是等比数列。 |
D.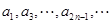 和 和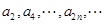 均是等比数列,且公比相同。 均是等比数列,且公比相同。 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com