
| 1-sinx |
| 1+sinx |
| 性质 | 理由 | 结论 | 得分 |
| 定义域 | |||
| 值域 | |||
| 奇偶性 | |||
| 周期性 | |||
| 单调性 | | ||
| 对称性 | |||
| 作图 |
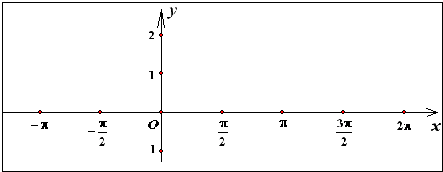 |
||
| 2 |
| kπ |
| 2 |
| 1-sinx |
| 1+sinx |
| 2 |
| 1+sinx |
| 1-sinx |
| π |
| 2 |
| 1-sinx |
| 1+sinx |
| x |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 1-sinx |
| 1+sinx |
| x |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| kπ |
| 2 |
| 性质 | 理由 | 结论 | 得分 | |||||||||||||||||
| 定义域 | -1≤sinx≤1 | 定义域R | 1分 | |||||||||||||||||
| 值域 | y2=2+2|cosx|∈[2,4] | 值域[
|
2分 | |||||||||||||||||
| 奇偶性 | f(-x)=f(x) | 偶函数 | 1分 | |||||||||||||||||
| 周期性 | f(x+π)=f(x) | 周期T=π | 2分 | |||||||||||||||||
| 单调性 | f(x)=
|
在[kπ-
在[kπ , kπ+
|
2分 | |||||||||||||||||
| 对称性 | f(-x)=f(x),f(
|
关于直线x=
|
2分 | |||||||||||||||||
| 作图 | 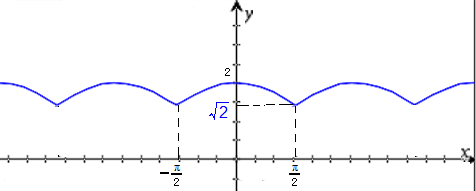 |
2分 | ||||||||||||||||||


科目:高中数学 来源: 题型:
| 1-sinx |
| 1+sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 7π |
| 12 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2014届广东罗定高一下学期期中质检数学试卷(多校联考)(解析版) 题型:解答题
函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性等,请选择适当的探究顺序,研究函数f(x)=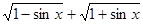 的性质,并在此基础上,作出其在
的性质,并在此基础上,作出其在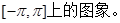
查看答案和解析>>
科目:高中数学 来源:甘肃省10-11学年高一下学期期末考试数学 题型:解答题
(本小题12分)函数的性质通常指函数的定义域、值域、奇偶性、周期性、单调性等,请选择适当的探究顺序,研究函数f(x)= 的性质,并在此基础上,作出其在
的性质,并在此基础上,作出其在 上的图像.
上的图像.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com