练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知M、N是两个平行平面，在M内取4个点，在N内取5个点，这9个点中再无其他4点共面，则

    (1)这些点最多能确定几个平面？

    (2)以这些点为顶点，能作多少个四棱锥，多少个三棱锥？

    答案：
    解析：

    		 　　(1)72个平面

    　　(1)72个平面

    　　(2)可构成25个四棱锥


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：走向清华北大同步导读·高二数学(上) 题型：044

    已知M(，a)，N(a，)，O为坐标原点，若直线OM的倾斜角是直线ON倾斜角的两倍，试求实数a以及直线MN的倾斜角．

    查看答案和解析>>

    科目：高中数学 来源：走向清华北大同步导读·高二数学(上) 题型：044

    已知点M(2，1)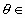，(0，)，并且直线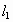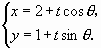：(t为参数)和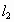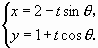：(t为参数)分别交x轴正半轴于点A，交y轴正半轴于点B，将四边形OAMB的面积记为S，其中O为坐标原点．

    （1）将S表示成 的函数，S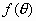＝，并指出函数的定义域D；

    （2）求函数S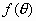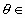＝，D的值域．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    已知M＝(1＋cos2x，1)，N＝(1，sin2x＋a)，(x∈R，a∈R，a是常数)，且y＝(O为坐标原点)

    (1)求y关于x的函数关系式y＝f(x)；

    (2)若x∈[0，]时，f(x)的最大值为4，求a的值，并说明此时f(x)的图像可由y＝2sin(x＋)的图像经过怎样的变换而得到．

    查看答案和解析>>

    科目：高中数学 来源：2007届莆田四中高三第四次月考数学试卷(理科) 题型：044

    解答题

    已知M(2,1),N(1,)(,是常数)，且(O是坐标原点)．

    (1)

    求关于的函数关系式；

    (2)

    若x∈［,］时，的最小值为2，求的值，并指出的单调增区间和说明()的图像可由的图像经过怎样的变换而得到．

    查看答案和解析>>

    同步练习册答案