
如图所示,A、F分别是椭圆![]() =1的一个顶点与一个焦点,位于x轴的正半轴上的动点T(t,0)与F的连线交射影OA于Q.求:
=1的一个顶点与一个焦点,位于x轴的正半轴上的动点T(t,0)与F的连线交射影OA于Q.求: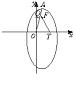
(1)点A、F的坐标及直线TQ的方程;
(2)△OTQ的面积S与t的函数关系式S=f(t)及其函数的最小值;
(3)写出S=f(t)的单调递增区间,并证明之.
解:(1)A点的坐标为(1,3),F点的坐标为(1,1) 当t>0且t≠1时,TQ的方程为y= 当t=1时,TQ的方程为x=1. (2)联立直线OA和直线TQ的方程;
得Q点的纵坐标为yQ= ∵t>0,且yQ>1,∴t> ∴f(t)= ∴f(t)= ∵t> 当且仅当t= (3)f(t)= 证明:任取t1、t2∈( f(t1)-f(t2)= = = ∵t2>t1> ∴S=f(t)在( |


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
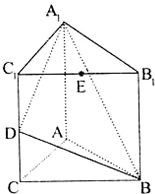 直三棱柱A1B1C1-ABC的三视图如图所示,D、E分别为棱CC1和B1C1的中点.
直三棱柱A1B1C1-ABC的三视图如图所示,D、E分别为棱CC1和B1C1的中点.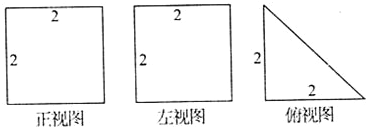
查看答案和解析>>
科目:高中数学 来源: 题型:
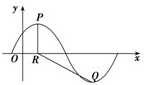 已知函数f(x)=Asin (
已知函数f(x)=Asin (| π |
| 3 |
| π |
| 2 |
| 2π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
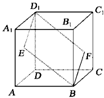
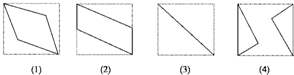 如图所示,E、F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是如图中的
如图所示,E、F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是如图中的查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省南昌十六中高三(上)11月月考数学试卷(理科)(解析版) 题型:选择题

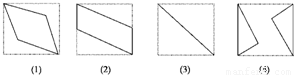
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com