练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设f（z）=2z（cos
    π
    6
    +icos
    2π
    3
    ），这里z是复数，用A表示原点，B表示f （1+
    		3
    i）所对应的点，C表示点-4i所对应的点，则∠ABC=
    30°
    30°
    ．
    分析：先求得f （1+
    		3
    i）=2
    		3
    +2i，可得点B（2
    		3
    ，2）．再由点A和点C的坐标，可得
    BA
     和
    BC
     的坐标、模、以及 
    BA
    •
    BC
     的值，再根据 cos＜
    BA
    ，
    BC
    ＞=
    BA
    •
    BC
    |
    BA
    |•|
    BC
    |
     求得＜
    BA
    ，
    BC
    ＞的值，可得∠ABC的值．
    解答：解：∵f（z）=2z（cos
    π
    6
    +icos
    2π
    3
    ）=2z（
    		3
    2
    -
    1
    2
    i），
    ∴f （1+
    		3
    i）=2（1+
    		3
    i）•（
    		3
    2
    -
    1
    2
    i）=2
    		3
    +2i，故点B（2
    		3
    ，2）．
    再由点A（0，0），点C（0，-4），可得
    BA
    =（-2
    		3
    ，-2），
    BC
    =（-2
    		3
    ，-6），
    ∴
    BA
    •
    BC
    =12+12=24，|
    BA
    |=4，|
    BC
    |=4
    		3
    ，∴cos＜
    BA
    ，
    BC
    ＞=
    BA
    •
    BC
    |
    BA
    |•|
    BC
    |
    =
    		3
    2
    ，
    ∴＜
    BA
    ，
    BC
    ＞=30°，故∠ABC=30°，
    故答案为 30°
    点评：本题主要考查复数的代数表示及其几何意义，复数与复平面内对应点之间的关系，两个向量的夹角公式的应用，体现了转化的数学思想，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013年普通高等学校招生全国统一考试安徽卷理数 题型：013

    设i是虚数单位，是复数z的共轭复数，若I＝|x|f(x)＞0|·zi＋2＝2z，则z＝

    [　　]

    A．1＋i

    B．1－i

    C．－1＋i

    D．－1－i

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年浙江省宁波市余姚中学高二（下）期中数学试卷（理科）（解析版） 题型：填空题

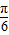    设f（z）=2z（cos+icos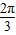），这里z是复数，用A表示原点，B表示f （1+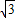i）所对应的点，C表示点-4i所对应的点，则∠ABC=    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设f(z)=2z(cos+icos)，这里z是复数，用A表示原点，B表示f(1+i)，C表示点-，则∠ABC=        。

    查看答案和解析>>

    同步练习册答案