

| C | 2 20 |
| C | 2 4 |
| C | 2 6 |
| C | 2 4 |
| C | 2 3 |
| C | 2 2 |
| 31 |
| 190 |
| ||
|
| 91 |
| 190 |
| ||||
|
| 42 |
| 95 |
| ||
|
| 3 |
| 38 |
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 91 |
| 190 |
| 42 |
| 95 |
| 3 |
| 38 |
| 3 |
| 5 |


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源:2013届江西省四校高二下学期第三次月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
医生的专业能力参数K可有效衡量医生的综合能力,K越大,综合能力越强,并规定:能力参数K不少于30称为合格,不少于50称为优秀,某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力参数K的频率颁布直方图:
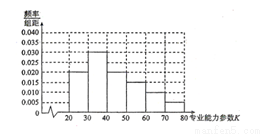
(1)求这个样本的合格率、优秀率,并估计能力参数K的平均值;
(2)现用分层抽样的方法从中抽出一个样本容量为20的样本,再从这20名医生中随机选出2名。
①求这2名医生的能力参数K为同一组的概率;
②设这2名医生中能力参数K为优秀的的人数为X,求随机变量X的分布列和期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
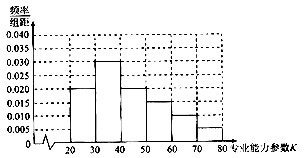
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省仙桃中学、麻城、新洲一中、武汉二中高二(上)期末数学试卷(理科)(解析版) 题型:解答题
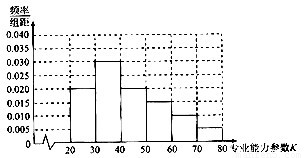
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com