
(12分)在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
附: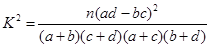 ;
;
 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:高中数学 来源: 题型:解答题
(本题满分12分)
为调查某工厂工人生产某种产品的能力,随机抽查了一些工人某天生产产品的数量,产品数量的分组区间为[45,55), [55,65), [65,75), [75,85), [85,95),由此得到频率分布直方图如图所示,保存中不慎丢失一些数据,但已知第一组 ([45,55) ]有4人;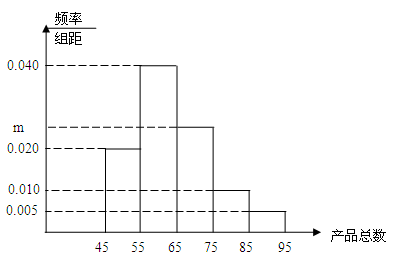
(Ⅰ)求被抽查的工人总人数n及图中所示m为多少;
(Ⅱ)求这些工人中一天生产该产品数量在[55,75)之间的人数是多少。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某校共有800名学生,高三一次月考之后,为了了解学生学习情况,用分层抽样方法从中抽出若干学生此次数学成绩,按成绩分组,制成如下的频率分布表:
| 组号 | 第 一 组 | 第 二 组 | 第 三 组 | 第 四 组 | 第 五 组 | 第 六 组 | 第 七 组 | 第 八 组 | 合计 |
| 分组 | 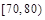 | 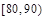 | 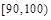 | 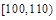 | 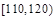 | 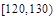 |  | 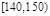 | |
| 频数 | 4 | 6 | 20 | 22 | 18 | 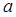 | 10 | 5 | 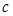 |
| 频率 | 0.04 | 0.06 | 0.20 | 0.22 | 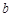 | 0.15 | 0.10 | 0.05 | 1 |
 ;
;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160 cm和184 cm之间,将测量结果按如下方式分成6组:第一组 [160,164],第二组[164,168],…,第6组[180,184],下图是按上述分组方法得到的频率分布直方图.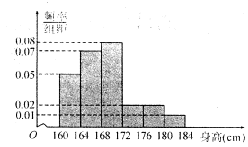
(Ⅰ)试评估该校高三年级男生在全市高中男生中的平均身高状况;
(Ⅱ)求这50名男生身高在172 cm以上(含172 cm)的人数;
(Ⅲ)在这50名男生身高在172 cm以上(含172 cm)的人中任意抽取2人,该2人中身高排名(从高到低)在全市前130名的人数记为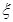 ,求
,求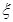 的数学期望.
的数学期望.
参考数据:
若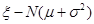 .则
.则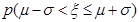 =0.6826,
=0.6826,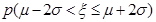 ="0.9544,"
="0.9544," 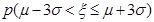 =0.9974.
=0.9974.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(11分)为了调查某厂2000名工人生产某种产品的能力,随机抽查了 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为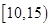 ,
,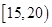 ,
,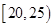 ,
,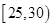 ,
,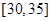 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在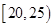 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求 ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工人不在同一组的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中 120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.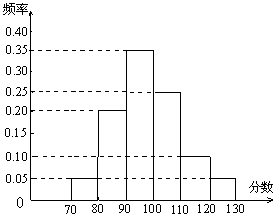
(1) 问各班被抽取的学生人数各为多少人?
(2) 在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的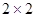 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为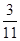 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 110 |
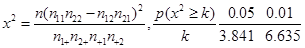 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表是关于某设备的使用年限(年)和所需要的维修费用y (万元)的几组统计数据:
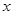 | 2 | 3 | 4 | 5 | 6 |
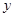 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
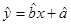 ;
;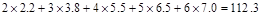 )
)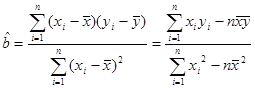 ;
;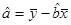 ;
; 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从高三学生中抽取50名同学参加数学竞赛,成绩的分组及各组的频数如下(单位:分):
[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100],8.
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)估计成绩在[60,90)分的学生比例.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com