
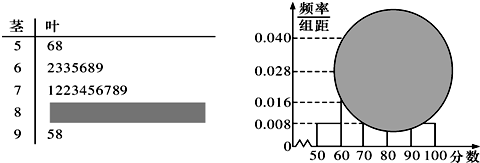
我校某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题.

(1)求全班人数及分数在[80,90)之间的频数;
(2)估计该班的平均分数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
解:(1)由茎叶图知,分数在[50,60)之间的频数为2,
频率为0.008×10=0.08 全班人数![]() =25
=25
所以分数在[80,90)之间的频数为25-2-7-10-2=4…………3分
(2)分数在[50,60)之间的总分数为56+58=114
分数在[60,70)之间的总分数为60×7+2+3+3+5+6+8+9=456
分数在[70,80)之间的总分数为70×10+1+2+2+3+4+5+6+7+8+9=747
分数在[80,90)之间的总分数为85×4=340分数在[90,100]之间的总分数为95+98=193
所以,该班的平均分数为![]() ……………5分
……………5分
估计平均分数时,以下解法也给分:
分数在[50,60)之间的频率为![]() =0.08分数在[60,70)之间的频率为
=0.08分数在[60,70)之间的频率为![]() =0.28
=0.28
分数在[70,80)之间的频率为![]() =0.40分数在[80,90)之间的频率为
=0.40分数在[80,90)之间的频率为![]() =0.16
=0.16
分数在[90,100]之间的频率为![]() =0.08所以该班的平均分数约为55×0.08+65×0.28+75×0.40+85×0.16+95×0.08 =73.8
=0.08所以该班的平均分数约为55×0.08+65×0.28+75×0.40+85×0.16+95×0.08 =73.8
所以频率分布直方图中[80,90)间的矩形的高为![]() ÷10=0.016………………8分
÷10=0.016………………8分
(3)将[80,90)之间的4个分数编号为1,2,3,4,[90,100]之间的2个分数编号为5,6,
在[80,100]之间的试卷中任取两份的基本事件为(1,2),(1,3),(1,4),(1,5)(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),共15个.
其中,至少有一份在[90,100]之间的基本事件有9个,故至少有一份分数在[90,100]之间的概率是![]() =0.6…
=0.6…
19(1)证明:依题意,知CA=CC1,又CD⊥AC1,所以,D为AC1的中点,
又F为CC1的中点,所以,DF∥AC,而AC![]() 平面ABC,所以,DF∥平面ABC,
平面ABC,所以,DF∥平面ABC,
同理可证:EF∥平面ABC,又DF![]() EF=F,所以,平面DEF∥平面ABC;...(6分)。(2)设AB=2,则DF=1,EF=2,∠DFE=60°,由余弦定理,求得:DE=
EF=F,所以,平面DEF∥平面ABC;...(6分)。(2)设AB=2,则DF=1,EF=2,∠DFE=60°,由余弦定理,求得:DE=![]() ,
,
又CD=![]() ,CE=
,CE=![]() ,所以,CD2+DE2=CE2,所以,CD⊥DE,
,所以,CD2+DE2=CE2,所以,CD⊥DE,
又CD⊥AC1,![]() DE=D,所以,CD⊥平面AEC1。
DE=D,所以,CD⊥平面AEC1。


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•汕头二模)某学校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程序的破坏,但可见部分如图,据此可以了解分数在[50,60)的频率为
(2013•汕头二模)某学校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程序的破坏,但可见部分如图,据此可以了解分数在[50,60)的频率为查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西新余第一中学高三第七次模拟考试文科数学试卷(解析版) 题型:解答题
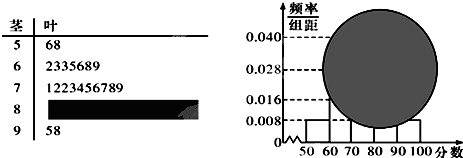
我校某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题.

(1)求全班人数及分数在[80,90)之间的频数;
(2)估计该班的平均分数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com