
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最值即可;
(2)问题转化为a>(x+2)[1-ln(1+x)],令h(x)=(x+2)[1-ln(1+x)],根据函数的单调性求出a的范围即可;
(3)当a=2,x>0时,得:$ln({1+x})>\frac{x}{x+2}(*)$,令$x=\frac{1}{k}({k∈{N^*}})$,得:$ln\frac{k+1}{k}>\frac{1}{2k+1}$,依次令k=1,2,3,…n,累加即可.
解答 解:(1)f(x)的定义域为$({-1,+∞}),f'(x)=\frac{1}{1+x}-1=-\frac{x}{1+x}.f'(x)>0?-1<x<0;f'(x)<0?x>0$,
所以函数f(x)的增区间为(-1,0),减区间为(0,+∞),
f(x)max=f(0)=0,无最小值.
(2)$?x>0,f(x)+g(x)>1??x>0,ln({1+x})-x+\frac{{{x^2}+2x+a}}{x+2}>1$
$??x>0,ln({1+x})+\frac{a}{x+2}>1??x>0,a>({x+2})[{1-ln({1+x})}]$,
令h(x)=(x+2)[1-ln(1+x)].
则$h'(x)=1-ln({1+x})-\frac{x+2}{x+1}=-ln({1+x})-\frac{1}{x+1}$.
当x>0时,显然$h'(x)=-ln({1+x})-\frac{1}{x+1}<0$,
所以h(x)在(0,+∞)上是减函数.
所以当x>0时,h(x)<h(0)=2.
所以,a的取值范围为[2,+∞).
(3)由(2)知,当a=2,x>0时,$ln({1+x})+\frac{2}{x+2}>1$,即$ln({1+x})>\frac{x}{x+2}(*)$.
在(*)式中,令$x=\frac{1}{k}({k∈{N^*}})$,得$ln\frac{k+1}{k}>\frac{{\frac{1}{k}}}{{2+\frac{1}{k}}}$,即$ln\frac{k+1}{k}>\frac{1}{2k+1}$,
依次令k=1,2,3,…n,
得$ln\frac{2}{1}>\frac{1}{3},ln\frac{3}{2}>\frac{1}{5},ln\frac{4}{3}>\frac{1}{7},…,ln\frac{n+1}{n}>\frac{1}{2n+1}$.
将这n个式子左右两边分别相加,
得$ln({n+1})>\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+…+\frac{1}{2n+1}$.
点评 本题考查利用导数研究函数的最值及单调性,解题过程中用到了分类讨论的思想,分类讨论的思想也是高考的一个重要思想,要注意体会其在解题中的运用,第3问难度比较大,是一道综合题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
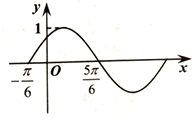 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则关于f(x)的说法正确的是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则关于f(x)的说法正确的是( )| A. | 对称轴方程是x=$\frac{π}{3}$+2kπ(k∈Z) | B. | φ=-$\frac{π}{6}$ | ||
| C. | 最小正周期为π | D. | 在区间($\frac{π}{2}$,$\frac{7π}{6}$)上单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 双曲线 | B. | 双曲线的一支 | C. | 一条射线 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
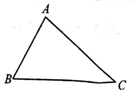
| A. | $5\sqrt{3}$ | B. | $6\sqrt{2}$ | C. | 8 | D. | $5\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com