
已知函数 .
.
(1)设 ,
, ,求
,求 的单调区间;
的单调区间;
(2)若对任意 ,
, ,试比较
,试比较 与
与 的大小.
的大小.
(1)单调递减区间是 ,单调递增区间是
,单调递增区间是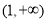 ;(2)
;(2) .
.
【解析】
试题分析:(1)根据题意,可以考虑利用导数来研究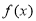 的单调性,当
的单调性,当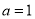 ,
, 时:
时: ,从而可得当
,从而可得当 时,
时,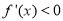 ,
,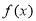 单调递减
单调递减
当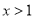 时,
时, ,
,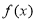 单调递增,因此
单调递增,因此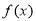 单调递减区间是
单调递减区间是 ,
,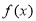 单调递增区间是
单调递增区间是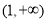 ;(2)由条件可知
;(2)由条件可知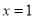 为
为 极小值点,从而有
极小值点,从而有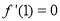 ,
,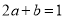 ,即
,即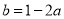 ,接下来考虑用作差法比较
,接下来考虑用作差法比较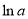 与
与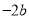 的大小关系,
的大小关系,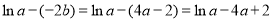 ,因此构造函数
,因此构造函数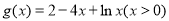 ,通过导数研究
,通过导数研究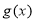 的单调性,从而判断
的单调性,从而判断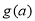 的取值情况:
的取值情况: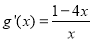 ,
,
令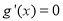 ,得
,得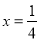 ,当
,当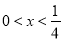 时,
时,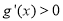 ,
,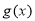 单调递增,当
单调递增,当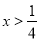 时,
时,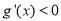 ,
,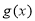 单调递减,
单调递减,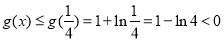 ,
,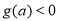 ,即
,即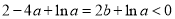 ,故
,故 .
.
试题解析:(1)由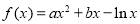 ,
,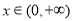 ,得
,得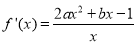 , 2分
, 2分
∵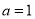 ,
,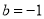 ,∴
,∴ , 3分
, 3分
令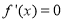 ,得
,得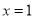 ,
,
当 时,
时,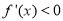 ,
,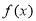 单调递减, 4分
单调递减, 4分
当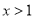 时,
时, ,
,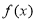 单调递增,
单调递增,
∴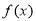 单调递减区间是
单调递减区间是 ,
,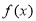 单调递增区间是
单调递增区间是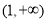 ; 6分
; 6分
(2)由题意可知,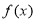 在
在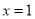 处取得最小值,即
处取得最小值,即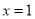 是
是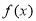 的极值点,
的极值点,
∴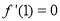 ,∴
,∴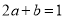 ,即
,即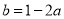 , 8分
, 8分
令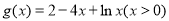 ,则
,则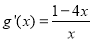 ,
,
令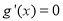 ,得
,得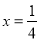 , 10分
, 10分
当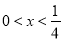 时,
时,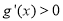 ,
,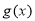 单调递增,
单调递增,
当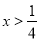 时,
时,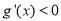 ,
,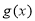 单调递减, 12分
单调递减, 12分
∴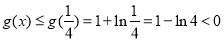 ,
,
∴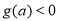 ,即
,即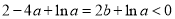 ,故
,故 . 14分.
. 14分.
考点:1.利用导数研究函数的单调性;2.函数与不等式综合.


科目:高中数学 来源:2015届湖北省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
以抛物线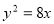 上的任意一点为圆心作圆与直线
上的任意一点为圆心作圆与直线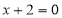 相切,这些圆必过一定点,则这一定点的坐标是( )
相切,这些圆必过一定点,则这一定点的坐标是( )
A.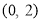 B.(2,0) C.(4,0) D.
B.(2,0) C.(4,0) D.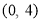
查看答案和解析>>
科目:高中数学 来源:2015届湖北省武汉市高三9月调考文科数学试卷(解析版) 题型:填空题
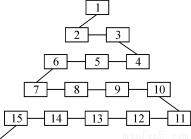
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行; ;依此类推,则
(1)按网络运作顺序第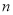 行第1个数(如第2行第1个数为2,第3行第1个数为4,
行第1个数(如第2行第1个数为2,第3行第1个数为4, )是 ;
)是 ;
(2)第63行从左至右的第3个数是 .
查看答案和解析>>
科目:高中数学 来源:2015届湖北省武汉市高三9月调考文科数学试卷(解析版) 题型:选择题
已知椭圆C: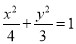 ,点M与C的焦点不重合.若M关于C的焦点的对称点分别为A,
,点M与C的焦点不重合.若M关于C的焦点的对称点分别为A,
B,线段MN的中点在C上,则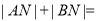 ( )
( )
A.4 B.8 C.12 D.16
查看答案和解析>>
科目:高中数学 来源:2015届湖北省高二4月月考数学试卷(解析版) 题型:填空题
复平面内有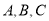 三点,点
三点,点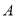 对应的复数为
对应的复数为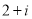 ,向量
,向量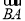 对应的复数为
对应的复数为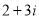 ,向量
,向量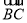 对应的复数为
对应的复数为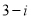 ,则点
,则点 对应的复数是___________.
对应的复数是___________.
查看答案和解析>>
科目:高中数学 来源:2015届湖北省高二5月月考理科数学试卷(解析版) 题型:填空题
某地区为了绿化环境进行大面积植树造林,如图,在区域  内植树,第一棵
内植树,第一棵
树在点Al(0,1),第二棵树在点.B1(l, l),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按
图中箭头方向每隔一个单位种一棵树,那么
(1)第n棵树所在点坐标是(44,0),则n= .
(2)第2014棵树所在点的坐标是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com