
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
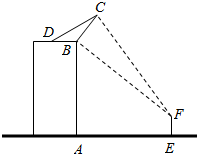 如图,一楼房高AB为19$\sqrt{3}$米,某广告公司在楼顶安装一块宽BC为4米的广告牌,CD为拉杆,广告牌的倾角为60°,安装过程中,一身高为$\sqrt{3}$米的监理人员EF站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设AE=x米,该监理人员观察广告牌的视角∠BFC=θ.
如图,一楼房高AB为19$\sqrt{3}$米,某广告公司在楼顶安装一块宽BC为4米的广告牌,CD为拉杆,广告牌的倾角为60°,安装过程中,一身高为$\sqrt{3}$米的监理人员EF站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设AE=x米,该监理人员观察广告牌的视角∠BFC=θ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com