归纳原理分别探求:
(1)凸n边形的内角和f(n)= ;
(2)凸n边形的对角线条数f(n)= ;
(3)平面内n个圆,其中每两个圆都相交于两点,且任意三个圆不相交于同一点,则该n个圆分平面区域数f(n)= .
【答案】
分析:本题考查的知识点是归纳推理(1)由三角形的内角和为180°,四边形的内角和为360°,五边形的内角和为540°,我们进行归纳推理,易得到结论;(2)我们由三角形有0条对角线,四边形有2条对角线,五边形有5条对角线,我们进行归纳推理,易得到结论;(3)我们由两个圆相交将平面分为4分,三个圆相交将平面分为8分,四个圆相交将平面分为14部分,我们进行归纳推理,易得到结论.
解答:解:(1)∵三角形的内角和为180°,
四边形的内角和为360°=2×180°,
五边形的内角和为540°=3×180°
…
故凸n边形的内角和f(n)=(n-2)180°
(2)∵三角形有0=
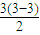
条对角线,
四边形有2=
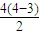
条对角线,
五边形有5=
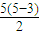
条对角线
…
凸n边形的对角线条数f(n)=

(3)∵一个圆将平面分为2份
两个圆相交将平面分为4=2+2份,
三个圆相交将平面分为8=2+2+4份,
四个圆相交将平面分为14=2+2+4+6份,
…
平面内n个圆,其中每两个圆都相交于两点,且任意三个圆不相交于同一点,则该n个圆分平面区域数f(n)=2+(n-1)n
故答案为:(n-2)180°,
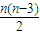
,2+(n-1)n
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

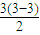 条对角线,
条对角线,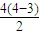 条对角线,
条对角线,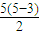 条对角线
条对角线
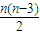 ,2+(n-1)n
,2+(n-1)n
