
(2006
湖北,20)设A、B分别为椭圆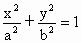 (a、b>0)的左、右顶点,椭圆长半轴的长等于焦距,且x=4为它的右准线.
(a、b>0)的左、右顶点,椭圆长半轴的长等于焦距,且x=4为它的右准线.
(1)
求椭圆的方程;(2)
设P为右准线上不同于点(4,0)的任意一点,若直线AP、BP分别与椭圆相交于异于A、B的点M、N,证明点B在以MN为直径的圆内(此题不要求在答题卡上画图).|
解析: (1)依题意得 解得 解得 从而 从而 , ,
故椭圆方程为  . .
(2) 解法一:由(1)得A(-2,0),B(2,0).设 . .
∵ M点在椭圆上,∴ . ① . ①
又 M点异于顶点A、B,∴ . .
由 P、A、M三点共线可得 . .
从而  , , . .
∴  . ② . ②
将①式代入②式简化得  . .
∵  ,∴ ,∴ .于是∠MBP为锐角,从而∠MBN为钝角,故点B在以MN为直径的圆内. .于是∠MBP为锐角,从而∠MBN为钝角,故点B在以MN为直径的圆内.
解法二:由 (1)得A(-2,0),B(2,0).设P(4,λ)(λ≠0),
 ,则直线AP的方程 ,则直线AP的方程 ,直线BP的方程为 ,直线BP的方程为 . .
∵点 M、N分别在直线AP、BP上,∴  , , . .
从而 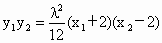 . ③ . ③
联立  消去y,得 消去y,得 . .
∵  ,―2是方程的两根,∴ ,―2是方程的两根,∴ , ,
即  . ④ . ④
又 
于是由③、④式代入⑤式化简可得  . .
∵ N点在椭圆上,且异于顶点A、B,∴ . .
又∵λ≠ 0,∴ ,从而 ,从而 , ,
故∠ MBN为钝角,即点B在以NM为直径的圆内.解法三:由 (1)得A(-2,0),B(2,0).设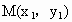 , , ,则 ,则 , , .又MN的中点Q的坐标为 .又MN的中点Q的坐标为 ,∴ ,∴
化简得  . ⑥ . ⑥
直线 AP的方程为 , ,
直线 BP的方程为 . .
∵点 P在准线x=4上,∴  ,即 ,即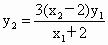 . ⑦ . ⑦
又∵ M点在椭圆上,∴  ,即 ,即 . ⑧ . ⑧
于是将⑦、⑧式代入⑥式化简可得
从而 B在以MN为直径的圆内. |
|
剖析:本题考查椭圆、圆以及直线与椭圆的位置关系,考查分析问题和解决问题的能力. |


 口算能手系列答案
口算能手系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com