
 如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°.
如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°. 解:(1)如图作AN⊥CD于N.
解:(1)如图作AN⊥CD于N. ,tan(45°-θ)=
,tan(45°-θ)= 
 =tan(45°-θ)=
=tan(45°-θ)=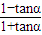
 =
=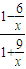 ,化简整理得x2-15x-54=0,
,化简整理得x2-15x-54=0, ,tanβ=
,tanβ= ,
,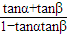




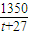 ,即t=
,即t= 时,α+β最小.
时,α+β最小. 时,α+β最小.
时,α+β最小.

科目:高中数学 来源: 题型:
 (2013•徐州一模)如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°.
(2013•徐州一模)如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°.查看答案和解析>>
科目:高中数学 来源: 题型:
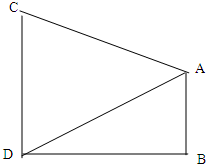 如图,两座建筑物AB,CD的高度分别为9m和15m,从建筑物AB的顶部看建筑物CD的张角∠CAD=45°.
如图,两座建筑物AB,CD的高度分别为9m和15m,从建筑物AB的顶部看建筑物CD的张角∠CAD=45°.查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三第一学期期中考试理科数学试卷(解析版) 题型:解答题
如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角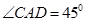 .
.
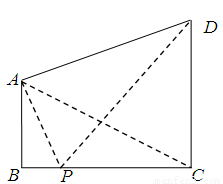
(1)求BC的长度;
(2)在线段BC上取一点P(点P与点B,C不重合),从点P看这两座建筑物的张角分别为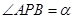 ,
,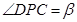 ,问点P在何处时,
,问点P在何处时,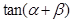 最小?
最小?
查看答案和解析>>
科目:高中数学 来源:2015届江苏省宝应县高一下学期期中考试数学试卷(解析版) 题型:解答题
如图,两座建筑物AB,CD的高度分别是9m和15m,从建筑物AB的顶部看建筑物CD的张角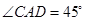 ,求建筑物AB和CD底部之间的距离BD
,求建筑物AB和CD底部之间的距离BD

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com