
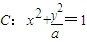 ,直线l:kx-y-k=0,O为坐标原点.
,直线l:kx-y-k=0,O为坐标原点.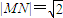 ,求曲线C的方程;
,求曲线C的方程;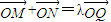 ?若存在,求实数λ的取值范围;若不存在,请说明理由.
?若存在,求实数λ的取值范围;若不存在,请说明理由.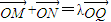 ,求得点Q的坐标,从而得出结论.
,求得点Q的坐标,从而得出结论.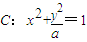 ,当a<0 时,曲线表示焦点在x 轴上的双曲线;
,当a<0 时,曲线表示焦点在x 轴上的双曲线; 得,(a+1)x2-2x+1-a=0,
得,(a+1)x2-2x+1-a=0,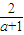 ,x1•x2=
,x1•x2=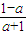 ,由弦长公式得
,由弦长公式得 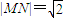 =
=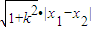
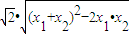 =
=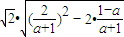 ,∴
,∴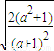 =1,
=1,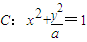 即 C:x2-y2=1,表示焦点在x轴上的等轴双曲线.
即 C:x2-y2=1,表示焦点在x轴上的等轴双曲线.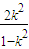 ,1×x2=
,1×x2=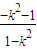 ,∴k=0.
,∴k=0.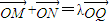 ,∴
,∴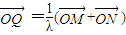 =
= ( 1+x2,0+y2)=
( 1+x2,0+y2)= ( 0,0)=(0,0).
( 0,0)=(0,0).

 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
| OA |
| OB |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
3
| ||
| 2 |
| 2 |
| ||
| 2 |
| m |
| BM |
| BN |
| BM |
| BN |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市十校高三(下)第二次联考数学试卷(理科)(解析版) 题型:解答题
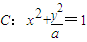 ,直线l:kx-y-k=0,O为坐标原点.
,直线l:kx-y-k=0,O为坐标原点.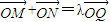 ?若存在,求实数λ的取值范围;若不存在,请说明理由;
?若存在,求实数λ的取值范围;若不存在,请说明理由;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com