练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知x，y，z满足（x-3）2+（y-4）2+z2=2，那么x2+y2+z2的最小值是    ．
    【答案】分析：利用球心与坐标原点的距离减去半径即可求出表达式的最小值．
    解答：解：由题意可得P（x，y，z），在以M（3，4，0）为球心，为半径的球面上，
    x2+y2+z2表示原点与点P的距离的平方，
    显然当O，P，M共线且P在O，M之间时，|OP|最小，
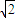
    此时|OP|=|OM|-=-=5，
    所以|OP|2=27-10．
    故答案为：27-10．
    点评：本题考查空间中两点间的距离公式的应用，考查计算能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知x，y，z满足方程x2+（y-2）2+（z+2）2=2，则
    		x2+y2+z2
    的最大值是（　　）
    A、3
    		2
    B、2
    		3
    C、4
    		2
    D、
    		2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知x，y，z满足
    x-y+5≥0
    x≤0
    x+y+k≥0
    ，且z=2x+4y的最小值为-6，则常数k的值为
    11
    3
    11
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知x，y，z满足
    x-y+5≥0
    x≤3
    x+y+k≥0
    ，且z=2x+4y    的最小值为-18，则常数k=
    23
    3
    23
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知x，y，z满足（x-3）2+（y-4）2+z2=2，那么x2+y2+z2的最小值是
    27-10
    		2
    27-10
    		2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知x、y、z满足不等式组, 则t=x2+y2+2x－2y+2的最小值为(     )

    A.          B.     C.3   D. 2

    查看答案和解析>>

    同步练习册答案