
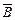 )+P(
)+P(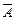 ·B)=0.24+0.24=0.48
·B)=0.24+0.24=0.48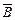 )+P(
)+P(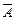 )·B]=0.36+0.48=0.84
)·B]=0.36+0.48=0.84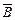 )=P(A)·P(
)=P(A)·P(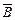 )=0.6×(1-0.6)=0.6×0.4=0.24
)=0.6×(1-0.6)=0.6×0.4=0.24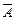 ·B)=P(
·B)=P(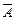 )P(B)=0.24,显然,“甲击中、乙未击中”和“甲未击中、乙击中”是不可能同时发生,即事件A·
)P(B)=0.24,显然,“甲击中、乙未击中”和“甲未击中、乙击中”是不可能同时发生,即事件A·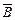 与
与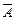 ·B互斥,所以恰有一人击中目标的概率是
·B互斥,所以恰有一人击中目标的概率是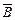 )+P(
)+P(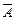 ·B)=0.24+0.24=0.48
·B)=0.24+0.24=0.48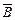 )+P(
)+P(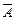 )·B]=0.36+0.48=0.84
)·B]=0.36+0.48=0.84

科目:高中数学 来源:不详 题型:解答题
 各人是否需使用设备相互独立.
各人是否需使用设备相互独立.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
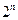 ,则算过关。问:(Ⅰ)某人在这项游戏中最多能过几关?(Ⅱ)他连过前三关的概率是多少?(注:骰子是一个在各面上分别有1,2,3,4,5,6点数的均匀正方体。抛掷骰子落地静止后,向上一面的点数为出现点数。)
,则算过关。问:(Ⅰ)某人在这项游戏中最多能过几关?(Ⅱ)他连过前三关的概率是多少?(注:骰子是一个在各面上分别有1,2,3,4,5,6点数的均匀正方体。抛掷骰子落地静止后,向上一面的点数为出现点数。)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 | |
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com