
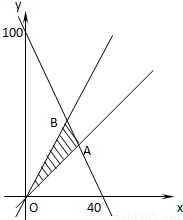
 解:设桌椅分别买x,y张,则桌椅的总数z=x+y…(2分)
解:设桌椅分别买x,y张,则桌椅的总数z=x+y…(2分)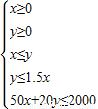 …(4分)
…(4分) ,
, ),B(25,37.5),
),B(25,37.5),

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)某实验中学高2010级同学共捐款2000元,准备为“希望小学”购买单价为50元的课桌和20元的椅子,若要使桌椅的总数尽可能多,但椅子数不能少于桌子数,且不多于桌子数的1.5倍,问桌椅各买多少才合适.(要求画出示意图)()
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)某实验中学高2010级同学共捐款2000元,准备为“希望小学”购买单价为50元的课桌和20元的椅子,若要使桌椅的总数尽可能多,但椅子数不能少于桌子数,且不多于桌子数的1.5倍,问桌椅各买多少才合适.(要求画出示意图)()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com