
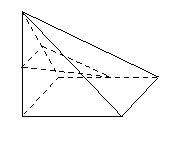
如右图所示,四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形, ![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求二面角D-FG-E的余弦值.
 |
(本小题主要考查空间线线关系.面面关系.空间向量及坐标运算等知识,考查数形结合.化归与转化的数学思想方法,以及空间想象能力.推理论证能力和运算求解能力)
(1)证法1:∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() .
.
又![]() 为正方形,
为正方形,
∴![]() .
.
∵![]() ,
,
∴![]() 平面
平面![]() .…………………4分
.…………………4分
∵![]() 平面
平面![]() , ∴
, ∴![]() .
.
∵![]() ,
,
∴![]() .…………………6分
.…………………6分
证法2:以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .…………………4分
.…………………4分
∵![]() ,
,
∴![]() .…………………6分
.…………………6分
(2)解法1:以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .…………………8分
.…………………8分
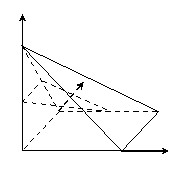
设平面DFG的法向量为![]() ,
,
∵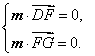
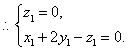
令![]() ,得
,得![]() 是平面
是平面![]() 的一个法向量.…………10分
的一个法向量.…………10分
设平面EFG的法向量为![]() ,
,
∵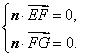
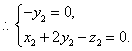
令![]() ,得
,得![]() 是平面
是平面![]() 的一个法向量.……………12分
的一个法向量.……………12分
∵![]()
![]()
![]()
![]() .
.
设二面角![]() 的平面角为θ,则
的平面角为θ,则![]() .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .…………………14分
.…………………14分
解法2:以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .…………………8分
.…………………8分
 |
过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,
∵![]() 三点共线,
三点共线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() ,解得
,解得![]() .…………………10分
.…………………10分
∴![]() . 再过
. 再过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,
∵![]() 三点共线,∴
三点共线,∴![]() ,
,
∵![]() , ∴
, ∴![]() ,
,
即![]() ,
,
解得![]() .∴
.∴![]() .
.
∴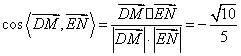 .…………………12分
.…………………12分
∵![]() 与
与![]() 所成的角就是二面角
所成的角就是二面角![]() 的平面角,
的平面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .…………………14分
.…………………14分


科目:高中数学 来源:2010-2011学年江西省南昌市高三第三次模拟考试理科数学 题型:解答题
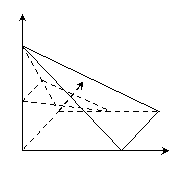
如右图所示,四棱锥P—ABCD中,底面ABCD为正方形,PD 平面ABCD,PD=AB=2,E,F,G分别为PC、PD、BC的中点。
平面ABCD,PD=AB=2,E,F,G分别为PC、PD、BC的中点。
(1)求证: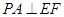 ;
;
(2)求二面角D—FG—E的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求证:BE⊥PD;
(2)求异面直线AE与CD所成角的大小.(用反三角函数表示)
查看答案和解析>>
科目:高中数学 来源:2011届江西省南昌市高三第三次模拟考试理科数学 题型:解答题
如右图所示,四棱锥P—ABCD中,底面ABCD为正方形,PD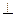 平面ABCD,PD=AB=2,E,F,G分别为PC、PD、BC的中点。
平面ABCD,PD=AB=2,E,F,G分别为PC、PD、BC的中点。
(1)求证: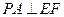 ;
;
(2)求二面角D—FG—E的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com