定义在R上的函数f(x),其图象是连续不断的,如果存在非零常数λ,(λ∈R,使得对任意的x∈R,都有f(x+λ)=λf(x),则称y=f(x)为“倍增函数”,λ为“倍增系数”,下列命题:
①函数f(x)=2x+11是倍增函数,且λ=1倍增系数;
②若函数y=f(x)是倍增系数λ=-1的倍增函数,则y=f(x)至少有1个零点;
③函数f(x)=e-x是倍增函数,且倍增系数λ∈(0,1).
其中为真命题的是 .(写出所有真命题的序号)
【答案】
分析:由f(x)=2x+11是倍增函数,知2(x+λ)+11=λ(2x+11),故由λ=
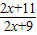
≠1,知①不正确;函数y=f(x)是倍增系数λ=-1的倍增函数,知f(x-1)=-f(x),由此得到y=f(x)至少有1个零点;由f(x)=e
-x是倍增函数,得到λ=
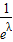
∈(0,1).
解答:解:∵f(x)=2x+11是倍增函数,
∴2(x+λ)+11=λ(2x+11),
∴λ=
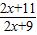
≠1,故①不正确;
∵函数y=f(x)是倍增系数λ=-1的倍增函数,
∴f(x-1)=-f(x),
当x=0时,f(-1)+f(0)=0,
若f(0),f(-1)任一个为0,函数f(x)有零点.
若f(0),f(-1)均不为零,则f(0),f(-1)异号,
由零点存在定理,在(-1,0)区间存在x
,f(x
)=0,
即y=f(x)至少有1个零点,故②正确;
∵f(x)=e
-x是倍增函数,
∴e
-(x+λ)=λe
-x,
∴
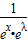
=
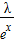
,
∴λ=
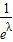
∈(0,1),故③正确.
故答案为:②③.
点评:本题考查命题的真假判断,解题时要认真审题,仔细解答,注意新定义的合理运用,合理地地进行等价转化.

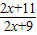 ≠1,知①不正确;函数y=f(x)是倍增系数λ=-1的倍增函数,知f(x-1)=-f(x),由此得到y=f(x)至少有1个零点;由f(x)=e-x是倍增函数,得到λ=
≠1,知①不正确;函数y=f(x)是倍增系数λ=-1的倍增函数,知f(x-1)=-f(x),由此得到y=f(x)至少有1个零点;由f(x)=e-x是倍增函数,得到λ=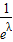 ∈(0,1).
∈(0,1).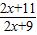 ≠1,故①不正确;
≠1,故①不正确;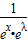 =
=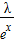 ,
,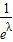 ∈(0,1),故③正确.
∈(0,1),故③正确.
