
【题目】选修4-5:不等式选讲
已知函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若不等式![]() 的解集为空集,求
的解集为空集,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用零点分类讨论法求不等式![]() 的解集;(2)由题得|x+1|-|x-a|<2a恒成立,再求出
的解集;(2)由题得|x+1|-|x-a|<2a恒成立,再求出![]() , 解不等式a+1<2a得解.
, 解不等式a+1<2a得解.
(1)当a=2时,不等式![]() ,即|x+1|-|x-2|>2,
,即|x+1|-|x-2|>2,
当![]() 时,原不等式可化为-x-1+x-2>2,即-3>2,此时原不等式无解;
时,原不等式可化为-x-1+x-2>2,即-3>2,此时原不等式无解;
当![]() 时,原不等式可化为x+1+x-2>2,解得
时,原不等式可化为x+1+x-2>2,解得![]() ,所以
,所以![]() ;
;
当x>2时,原不等式可化为x+1-x+2>2,即3>2,此时原不等式恒成立,
所以x>2;
综上,原不等式的解集为![]() .
.
(2)由![]() 的解集为空集得
的解集为空集得![]() 的解集为空集,
的解集为空集,
所以|x+1|-|x-a|<2a恒成立.
因为![]() ,所以
,所以![]() ,
,
所以当且仅当![]() 即
即![]() 时,
时,![]() ,
,
所以a+1<2a,
解得a>1,
即![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】《中国诗词大会》是央视推出的一档以“赏中华诗词,寻文化基因,品生活之美”为宗旨的大型文化类竞赛节目,邀请全国各个年龄段、各个领域的诗词爱好者共同参与诗词知识比拼。“百人团”由一百多位来自全国各地的选手组成,成员上至古稀老人,下至垂髫小儿,人数按照年龄分组统计如下表:
分组(年龄) |
|
|
|
频数(人) |
|
|
|
(1)用分层抽样的方法从“百人团”中抽取![]() 人参加挑战,求从这三个不同年龄组中分别抽取的挑战者的人数;
人参加挑战,求从这三个不同年龄组中分别抽取的挑战者的人数;
(2)在(1)中抽出的![]() 人中,任选
人中,任选![]() 人参加一对一的对抗比赛,求这
人参加一对一的对抗比赛,求这![]() 人来自同一年龄组的概率。
人来自同一年龄组的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,E为AB的中点.将
,E为AB的中点.将![]() 沿CE折起,使点B到达点F的位置,且平面CEF与平面ADCE所成的二面角为
沿CE折起,使点B到达点F的位置,且平面CEF与平面ADCE所成的二面角为![]() .
.
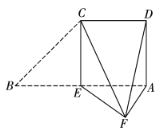
(1)求证:平面![]() 平面AEF;
平面AEF;
(2)求直线DF与平面CEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某学校研究性课题《什么样的活动最能促进同学们进行垃圾分类》向题的统计图(每个受访者都只能在问卷的5个活动中选择一个),以下结论错误的是( )

A. 回答该问卷的总人数不可能是100个
B. 回答该问卷的受访者中,选择“设置分类明确的垃圾桶”的人数最多
C. 回答该问卷的受访者中,选择“学校团委会宣传”的人数最少
D. 回答该问卷的受访者中,选择“公益广告”的人数比选择“学校要求”的少8个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个说法,其中正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“双曲线
”是“双曲线![]() 的离心率大于
的离心率大于![]() ”的充要条件
”的充要条件
C.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.命题“在![]() 中,若
中,若![]() ,则
,则![]() 是锐角三角形”的逆否命题是假命题
是锐角三角形”的逆否命题是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥![]() 中,O为顶点S在底面ABCD内的投影,P为侧棱SD的中点,且
中,O为顶点S在底面ABCD内的投影,P为侧棱SD的中点,且![]() .
.
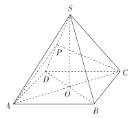
(1)证明:![]() 平面PAC.
平面PAC.
(2)求直线BC与平面PAC的所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从分别写有数字1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数字不大于第二张卡片的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从6名男医生和3名女医生中选出5人组成一个医疗小组,请解答下列问题:
(1)如果这个医疗小组中男女医生都不能少于2人,共有多少种不同的建组方案?(用数字作答)
(2)男医生甲要担任医疗小组组长,所以必选,而且医疗小组必须男女医生都有,共有多少种不同的建组方案?
(3)男医生甲与女医生乙不被同时选中的概率.(化成最简分数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com