练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知正数a，b满足3ab+a+b=1，则ab 的最大值是    ．
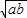
    【答案】分析：由3ab+a+b=1得到a+b=1-3ab，因为a，b为正数，所以利用基本不等式a+b≥2 得到不等式，求出解集即可得到ab的最大值；
    解答：解：因为a，b为正数，所以由基本不等式化简得：1-3ab=a+b≥2 ，
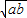
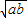
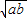
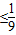
    所以3ab+2 -1≤0，≤，ab，当且仅当a=b时等号成立，
    得到ab的最大值是；
    故答案为．
    点评：此道题的方法实质是利用基本不等式将等式转化为不等式后，解不等式；而不是直接用基本不等式放缩得到最值，因此不存在放缩后是否为定值的问题．要求学生灵活运用基本不等式求函数的最值．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （Ⅰ）若a，b∈R，试证：a2+b2≥2（a+b-1）；
    （Ⅱ）已知正数a，b满足2 a2+3 b2=9，求证：a
    		1+b2
    ≤
    		6
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）已知正数a、b满足a+b=1．求：
    1
    a
    +
    2
    b
    的最小值．
    （2）若正实数x、y满足x+y+3=xy，求xy的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知正数a，b满足
    9
    a
    +
    1
    b
    =3，则ab的最小值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （1）已知正数a、b满足a+b=1．求：数学公式的最小值．
    （2）若正实数x、y满足x+y+3=xy，求xy的最小值．

    查看答案和解析>>

    科目：高中数学 来源：福建省厦门六中09-10学年高一下学期期中考试 题型：解答题

     已知正数a，b满足ab=a+b+3，求ab的取值范围。

     

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案