
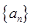 的首项
的首项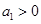 ,公比
,公比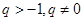 ,设数列
,设数列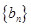 的通项公式
的通项公式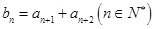 ,数列
,数列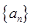 ,
,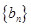 的前
的前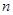 项和分别记为
项和分别记为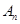 ,
,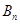 ,试比较
,试比较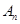 与
与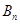 的大小.
的大小.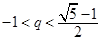 且
且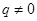 时,
时,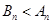 ;当
;当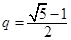 时,
时,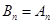 ;当
;当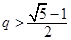 时,
时,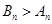 .
.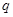 是否等于1.可以先将等比数列
是否等于1.可以先将等比数列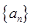 的前
的前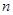 项和
项和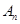 表示出来,再将
表示出来,再将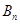 用
用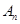 表示出来.以
表示出来.以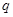 是否等于1分两大类讨论
是否等于1分两大类讨论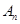 与
与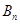 的大小.
的大小.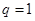 由
由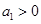 易知
易知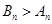 ;
;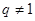 ,用作差法讨论
,用作差法讨论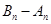 的正负以比较大小关系.注意将
的正负以比较大小关系.注意将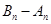 写成几个因式的乘积,通过判断各因式的正负来定
写成几个因式的乘积,通过判断各因式的正负来定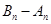 的正负.最后结合两大类讨论的情况作一总结.
的正负.最后结合两大类讨论的情况作一总结.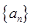 的首项
的首项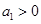 ,公比
,公比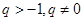 ,所以其前
,所以其前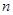 项和
项和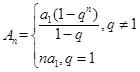 .
.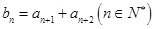 ,所以数列
,所以数列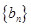 的前
的前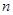 项和
项和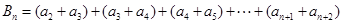
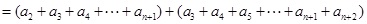

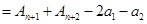
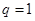 时,
时, ,
,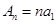 ,因为
,因为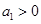 ,
,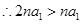 ,
,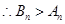 4分
4分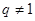 时,
时,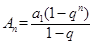 ,
,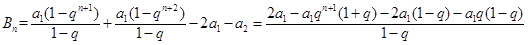
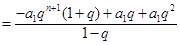
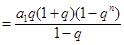 .
.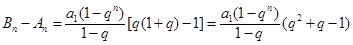 .令
.令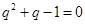 ,
,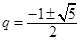 ,又因为
,又因为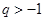 ,所以
,所以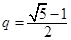 .因为
.因为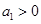 ,当
,当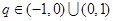 时,
时,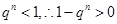 ,
,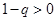 ,所以
,所以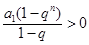 ,当
,当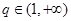 时,
时,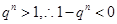 ,
,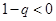 ,所以
,所以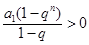 .故当
.故当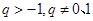 时,恒有
时,恒有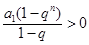
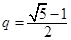 时,
时,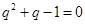 ,此时
,此时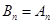 10分
10分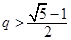 且
且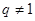 时,
时,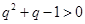 ,此时
,此时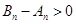 ,即
,即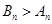 12分
12分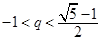 且
且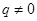 时,
时,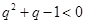 ,此时
,此时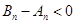 ,即
,即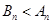 14分
14分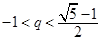 且
且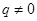 时,
时,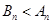 ;当
;当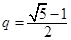 时,
时,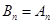 ;当
;当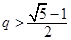 时,
时,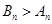 . 16分
. 16分 项和;2.作差法比较大小;3.一元二次不等式与相应的二次方程的联系.
项和;2.作差法比较大小;3.一元二次不等式与相应的二次方程的联系.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com