
定义在 上的函数
上的函数 满足下列两个条件:
满足下列两个条件:
⑴对任意的 恒有
恒有 成立; ⑵当
成立; ⑵当 时,
时, ;
;
记函数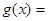
 ,若函数
,若函数 恰有两个零点,则实数
恰有两个零点,则实数 的取值范围是 ( )
的取值范围是 ( )
A.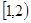 | B. | C. | D. |
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:单选题
已知函数
 的最小正周期为
的最小正周期为 ,为了得到函数
,为了得到函数
 的图象,只要将
的图象,只要将 的图象( )
的图象( )
A.向左平移 个单位长度 个单位长度 | B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 | D.向右平移 个单位长度 个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知函数 与
与 的图像在
的图像在 上不间断,由下表知方程f(x)=g(x)有实数解的区间是( )
上不间断,由下表知方程f(x)=g(x)有实数解的区间是( )
| x | -1 | 0 | 1 | 2 | 3 |
| f(x) | -0.677 | 3.011 | 5.432 | 5.980 | 7.651 |
| g(x) | -0.530 | 3.451 | 4.890 | 5.241 | 6.892 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知函数 与
与 的图像在
的图像在 上不间断,由下表知方程
上不间断,由下表知方程 有实数解的区间是( )
有实数解的区间是( )
 | -1 | 0 | 1 | 2 | 3 |
 | -0.677 | 3.011 | 5.432 | 5.980 | 7.651 |
 | -0.530 | 3.451 | 4.890 | 5.241 | 6.892 |
 B.
B. C.
C.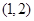 D.
D.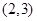
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
对实数a与b,定义新运算“?”: .设函数f(x)=(x2﹣2)?(x﹣x2),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
.设函数f(x)=(x2﹣2)?(x﹣x2),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
A.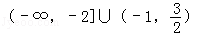 |
B.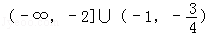 |
C. |
D.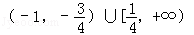 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
若 ,则函数
,则函数 的两个零点分别位于区间( )
的两个零点分别位于区间( )
| A.(a,b)和(b,c)内 |
| B.(-∞,a)和(a,b)内 |
| C.(b,c)和(c,+∞)内 |
| D.(-∞,a)和(c,+∞)内 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com