练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数y=-|x2-3x+2|的单调递增区间是________．

    （-∞，1]和
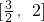
    分析：画出函数y=|x2-3x+2|的图象，结合图象写出函数y=|x2-3x+2|的递减区间即得到函数y=-|x2-3x+2|的单调递增区间
    解答：因为函数y=|x2-3x+2|的图象为：

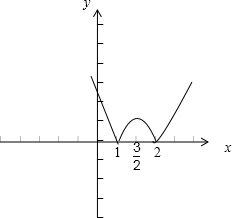
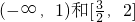
    所以函数y=|x2-3x+2|在递减，
    所以函数y=-|x2-3x+2|的单调递增区间是（-∞，1]和．
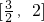
    故答案为：（-∞，1]和．
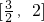
    点评：求函数的单调区间，若函数的图象是基本初等函数或由基本初等函数变换而来的，可先画出图象，结合图象写出单调区间．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    12、在直角坐标系中，函数y=x2-3|x|+1的图象关于
    y轴
    对称．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    13、函数y=x2-3|x-1|-1的图象与x轴不同的交点的个数共有（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求函数y=
    		x2-3
    -
    		5-x2
    +（x-2）0的定义域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数y=x2+3在x=1处的导数是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    函数y=x2-3|x-1|-1的图象与x轴不同的交点的个数共有（　　）
    A．4个B．3个C．2个D．1个

    查看答案和解析>>

    同步练习册答案