
 ,AF=1,M是EF的中点.
,AF=1,M是EF的中点.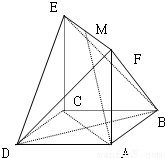
 ,
,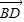 ,
, ,根据
,根据 •
• =0,
=0,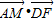 =0可得AM⊥BD,AM⊥DF,而BD∩DF=D,根据线面垂直的判定定理可证得AM⊥平面BDF;
=0可得AM⊥BD,AM⊥DF,而BD∩DF=D,根据线面垂直的判定定理可证得AM⊥平面BDF; =t
=t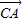 (0≤t≤1),求出
(0≤t≤1),求出 ,
, ,根据直线PF与CD所成的角为60°建立等式求出t的值,从而确定点P的位置.
,根据直线PF与CD所成的角为60°建立等式求出t的值,从而确定点P的位置.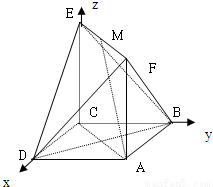 (Ⅰ)证明:设底面对角线的交点为O,连接E、O. …(1分)
(Ⅰ)证明:设底面对角线的交点为O,连接E、O. …(1分) ,
, ,0),M(
,0),M( ,
, ,1),B(0,
,1),B(0, ,0),D(
,0),D(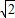 ,0,0),F(
,0,0),F( ,
,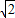 ,1),
,1), =(-
=(- ,-
,- ,1),
,1),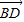 =(
=( ,-
,- ,0),
,0),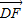 =(0,
=(0, ,1),
,1), •
•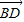 =0,
=0,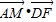 =0
=0 ,
, ,0),D(
,0),D(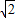 ,0,0),F(
,0,0),F( ,
, ,1),
,1),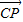 =t
=t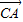 (0≤t≤1)即
(0≤t≤1)即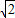 ,
, ,0)=(
,0)=(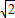 t,
t, t,0)
t,0) t,
t, t,0)…(10分)
t,0)…(10分) =(
=(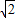 -
- ,
, -
-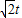 ,1),
,1),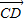 =(
=(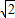 ,0,0),
,0,0),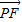 ,
, >=
>= (0≤t≤1)
(0≤t≤1) 或t=
或t= (舍)
(舍)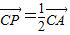


科目:高中数学 来源: 题型:
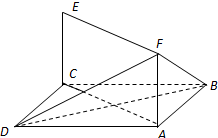 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
| PF |
| DA |
查看答案和解析>>
科目:高中数学 来源: 题型:
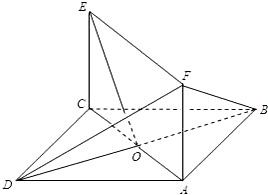 如图所示,正方形ABCD和矩形ACEF所在的平面相互垂直,已知AB=2,AF=
如图所示,正方形ABCD和矩形ACEF所在的平面相互垂直,已知AB=2,AF=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
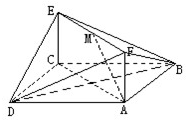 已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com