
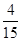 .
.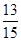 .
.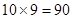 种抽法 3分
种抽法 3分 ,则事件
,则事件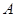 含有的基本事件数为
含有的基本事件数为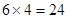 5分
5分 7分
7分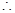 甲抽到选择题,乙抽到判断题的概率是
甲抽到选择题,乙抽到判断题的概率是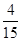 . 8分
. 8分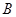 ,其对立事件为“甲、乙二人都抽到判断题”,记为事件
,其对立事件为“甲、乙二人都抽到判断题”,记为事件 ,则事件
,则事件 含有的基本事件数为
含有的基本事件数为 10分
10分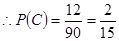
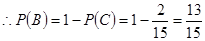 12分
12分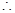 甲、乙二人中至少有一人抽到选择题的概率是
甲、乙二人中至少有一人抽到选择题的概率是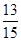 . 13分
. 13分

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:不详 题型:解答题
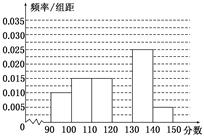
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
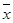 ;(II)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率
;(II)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率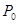 .
.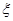 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量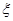 的分布列及数学期望
的分布列及数学期望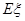 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
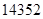 ”是一个五位波浪数。则从由
”是一个五位波浪数。则从由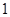 、
、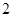 、
、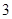 、
、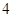 、
、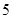 组成的没有重复数字的所有五位数中任意取一个数是五位波浪数的概率是( )
组成的没有重复数字的所有五位数中任意取一个数是五位波浪数的概率是( )A.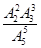 | B.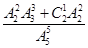 |
C.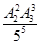 | D.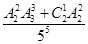 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
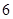 个面的中心,甲从这
个面的中心,甲从这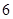 个点中任意选两个点连成直线,乙也从这
个点中任意选两个点连成直线,乙也从这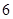 个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于( )
个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于( )A.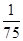 | B.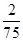 | C.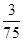 | D.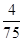 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
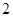 个红球和
个红球和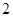 个黒球的口袋内任取
个黒球的口袋内任取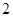 个球,互斥而不对立的两个事件是:
个球,互斥而不对立的两个事件是:| A.至少有一个黒球与都是黒球 | B.至少有一个红球与都是红球 |
C.至少有一个黒球与至少有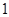 个红球 个红球 | D.恰有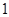 个黒球与恰有 个黒球与恰有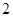 个黒球 个黒球 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com