
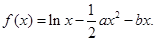
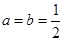 时,求函数
时,求函数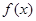 的最大值;
的最大值;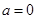 ,
,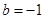 ,方程
,方程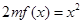 有唯一实数解,求正数
有唯一实数解,求正数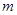 的值.
的值.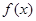 的极大值为
的极大值为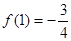 ,此即为最大值;(2)
,此即为最大值;(2) 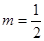 。
。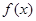 的定义域为(0,+∞),当
的定义域为(0,+∞),当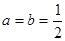 时,
时, ,
,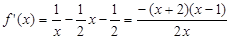 ……………2分
……………2分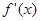 =0,解得
=0,解得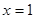 .(∵
.(∵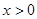 )
)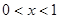 时,
时,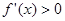 ,此时
,此时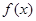 单调递增;当
单调递增;当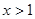 时,
时,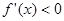 ,此时
,此时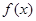 单调递减.
单调递减.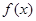 的极大值为
的极大值为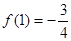 ,此即为最大值 ……………4分
,此即为最大值 ……………4分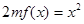 有唯一实数解,所以
有唯一实数解,所以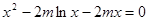 有唯一实数解,
有唯一实数解,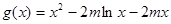 ,则
,则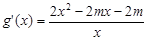 .令
.令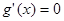 ,
,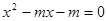 .
. 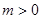 ,
,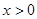 , 所以
, 所以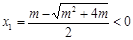 (舍去),
(舍去),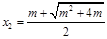 ,…… 6分
,…… 6分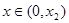 时,
时,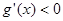 ,
,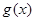 在(0,
在(0,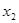 )上单调递减,
)上单调递减,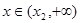 时,
时,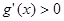 ,
,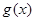 在(
在(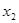 ,+∞)单调递增
,+∞)单调递增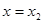 时,
时,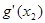 =0,
=0,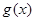 取最小值
取最小值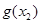 .
. 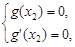 既
既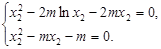 ……………10分
……………10分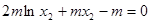 ,因为
,因为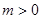 ,所以
,所以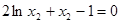 (*)
(*)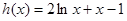 ,因为当
,因为当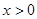 时,
时,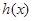 是增函数,所以
是增函数,所以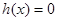 至多有一解.
至多有一解.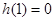 ,所以方程(*)的解为
,所以方程(*)的解为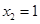 ,即
,即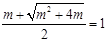 ,解得
,解得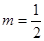 ………12分
………12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com