
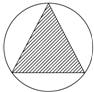
 某人随机地在如图所示正三角形及其外接圆区域内部投针(不包括三角形边界及圆的边界),则针扎到阴影区域(不包括边界)的概率为( )
某人随机地在如图所示正三角形及其外接圆区域内部投针(不包括三角形边界及圆的边界),则针扎到阴影区域(不包括边界)的概率为( ) 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013届云南省高二下学期期中理科数学试卷(解析版) 题型:填空题
某人随机地在如图所示正三角形及其外接圆内部区域投针(不包括三角形边界及其外接圆边界),则针扎到阴影区域(不包括边界)的概率为

查看答案和解析>>
科目:高中数学 来源:2012-2013学年广西柳州市铁路一中学高一(下)第一次月考数学试卷(解析版) 题型:选择题
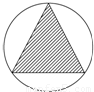
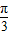
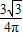
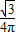
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com