Question

在科技馆里，小亮看见一台名为帕斯卡三角的仪器，如下图所示，当一实心小球从入口落下，它在依次碰到每层菱形挡块时，会等可能地向左或向右落下.

（1）试问小球通过第二层A位置的概率是多少？

（2）请用学过的数学方法模拟试验，并具体说明小球下落到第三层B位置和第四层C位置处的概率各是多少？

Answer 1

分析：本题若直接求基本事件的个数，按照现在学过的知识解决比较困难，我们可从树形图和列举法两种方法求基本事件的总数.

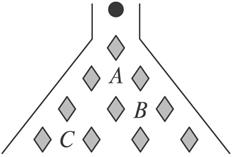
解法一：（1）实心小球在碰到菱形挡块时向左或向右下落是等可能性的,经过一个菱形挡块后向左或向右下落的概率各是原概率的一半.

画树状图可知，落到点A位置的概率为.

（2）同理可画树状图,得落到点B位置的概率为.

（3）同理可画树状图,得落到C点位置的概率为.

解法二：（1）实心小球碰到每个菱形挡块时向左或向右是等可能性的，因此小球下落到的可能性会有以下的途径｛左右，右左｝两种情况，而下落到第二层，共｛左左，左右，右左，右右｝四种情况.

由概率定义,得P(A)=.

（2）同理，到达第三层B位置会有以下途径｛左右右，右左右，右右左｝三种情况,而下落到第三层共有｛左左左，左左右，左右左，左右右，右左左，右左右，右右左，右右右｝八种情况.由概率定义，得P(B)=.

（3）同理，到达第四层C位置会有｛左左左右，左左右左，左右左左，右左左左｝四种情况,而下落到第四层共有｛左左左左，左左左右，左左右左，左右左左，右左左左，左右左右，左右右左，左左右右，右左左右，右左右左，右右左左，右右右左，右右左右，右左右右，左右右右，右右右右｝,共16种情况.

由概率定义,得P(C)=.

解法三：本题也可用贾宪三角方法，先算出小球下落路径条数，如下图.

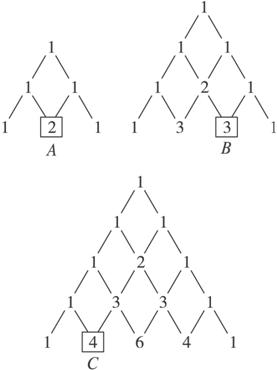
由题意知：小球经过每条路径的可能性相同.

由概率定义易得P(A)=，

P(B)=，

P(C)=.

绿色通道

    在解决较为抽象的问题时，借助于几何图形，可以非常直观、清晰地表达出问题的条件和结果，使抽象的思维找到着力点，在概率中利用树形图、列表法求基本事件总数，就是数形结合的典范.