
已知函数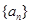 是首项为2,公比为
是首项为2,公比为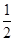 的等比数列,数列
的等比数列,数列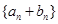 是首项为-2,第三项为2的等差数列.
是首项为-2,第三项为2的等差数列.
(1)求数列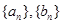 的通项式.
的通项式.
(2)求数列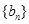 的前
的前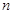 项和
项和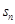 .
.
(1) 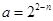 ,bn=2n-4-
,bn=2n-4-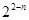 ; (2) Tn=n2-3n-4+
; (2) Tn=n2-3n-4+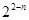 .
.
【解析】
试题分析:(1)直接用等比数列等差数列即可求得数列{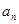 }{bn}的通项公式.
}{bn}的通项公式.
(2) 数列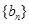 是一个等差数列与一个等比数列的和,故其求和采用分组求和的方法.
是一个等差数列与一个等比数列的和,故其求和采用分组求和的方法.
试题解析:(1)∵数列{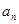 }是首项
}是首项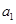 =2,公比q=
=2,公比q=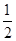 的等比数列,
的等比数列,
∴an=2·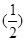 n-1=22-n,
n-1=22-n,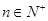 3分
3分
依题意得数列{bn+an}的公差d=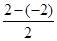 =2,
=2,
∴bn+an=-2+2(n-1)=2n-4,
∴bn=2n-4-22-n ,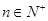 6分
6分
(2) 设Sn为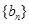 的前n项和,由(1)得 Sn=
的前n项和,由(1)得 Sn=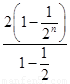 =4
=4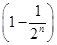 9分
9分
设数列{bn+an}的前n项和为Pn 则 Pn=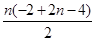 =n(n-3),
=n(n-3),
∴Tn=Pn-Sn=n(n-3)-4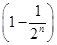 =n2-3n-4+22-n
12分
=n2-3n-4+22-n
12分
考点:等差数列等比数列的通项公式及前n项和公式


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年上海市静安、杨浦、青浦、宝山区高考数学二模试卷(文理合卷)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com