
(8分)有4个不同的球,四个不同的盒子,把球全部放入盒内.
(1)共有多少种放法?
(2)恰有一个盒子不放球,有多少种放法?
(3)恰有两个盒不放球,有多少种放法?
(1)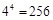 ;(2)
;(2)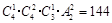 ;(3)
;(3) .
.
【解析】(1)利用分布乘法原理求解即可;(2)先选一个特称的盒子,然后利用分步原理求解;(3)先二个特殊盒子,然后把球分堆,最后利用分布乘法原理求解即可。
解:(1)一个球一个球地放到盒子里去,每只球都可有4种独立的放法,由分步乘法计数原理,放法共有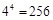 种.
种.
(2)为保证“恰有一个盒子不放球”,先从四个盒子中任意拿出去1个,即将4个球分成2,1,1的三组,有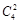 种分法;然后再从三个盒子中选一个放两个球,其余两个球,两个盒子,全排列即可.由分步乘法计数原理,共有放法:
种分法;然后再从三个盒子中选一个放两个球,其余两个球,两个盒子,全排列即可.由分步乘法计数原理,共有放法: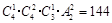 种.
种.
(3)先从四个盒子中任意拿走两个有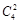 种,问题转化为:“4个球,两个盒子,每盒必放球,有几种放法?”从放球数目看,可分为(3,1),(2,2)两类.第一类:可从4个球中先选3个,然后放入指定的一个盒子中即可,有
种,问题转化为:“4个球,两个盒子,每盒必放球,有几种放法?”从放球数目看,可分为(3,1),(2,2)两类.第一类:可从4个球中先选3个,然后放入指定的一个盒子中即可,有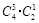 种放法;第二类:有
种放法;第二类:有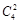 种放法.因此共有
种放法.因此共有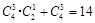 种.由分步乘法计数原理得“恰有两个盒子不放球”的放法有:
种.由分步乘法计数原理得“恰有两个盒子不放球”的放法有: 种.
种.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(08年鄂尔多斯市一模理) 袋中有4个不同红球,6个不同白球,若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不少于8分的取法有 ( )
A.6 B.60 C.66 D.186
查看答案和解析>>
科目:高中数学 来源:2013届福建省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
(本小题8分)
一个口袋内有4个不同的红球,6个不同的白球.
(1)从中任取4个球,红球的个数不比白球少的取法有多少种?
(2)若取一个红球记2分,取一个白球记1分,从中任取4个球,使总分不少于7分的取法有多少种?
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市嘉定区高三年级第一次质量调研理科数学 题型:解答题
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知函数 (
( )在区间
)在区间 上有最大值
上有最大值 和最小值
和最小值 .设
.设 .
.
(1)求 、
、 的值;
的值;
(2)若不等式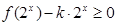 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(3)若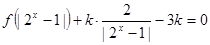 有三个不同的实数解,求实数
有三个不同的实数解,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:上海市长宁区2010届高三第二次模拟考试数学理 题型:解答题
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
在平行四边形 中,已知过点
中,已知过点 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若 。
。
(1)求证: 与
与 的关系为
的关系为 ;
;
(2)设 ,定义函数
,定义函数 ,点列
,点列 在函数
在函数 的图像上,且数列
的图像上,且数列 是以首项为1,公比为
是以首项为1,公比为 的等比数列,
的等比数列, 为原点,令
为原点,令 ,是否存在点
,是否存在点
 ,使得
,使得 ?若存在,请求出
?若存在,请求出 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。
(3)设函数 为
为 上偶函数,当
上偶函数,当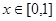 时
时 ,又函数
,又函数 图象关于直线
图象关于直线 对称, 当方程
对称, 当方程 在
在 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com