
 如图所示的方格纸中有定点O,P,Q,A,B,C,D,则$\overrightarrow{OP}$+$\overrightarrow{OQ}$=( )
如图所示的方格纸中有定点O,P,Q,A,B,C,D,则$\overrightarrow{OP}$+$\overrightarrow{OQ}$=( )| A. | $\overrightarrow{OA}$ | B. | $\overrightarrow{OB}$ | C. | $\overrightarrow{CO}$ | D. | $\overrightarrow{DO}$ |
分析 可设一个小方格的边长为1,从而可以得出图中各点的坐标,进而得出向量$\overrightarrow{OP}+\overrightarrow{OQ}$的坐标,容易看出$\overrightarrow{OP}+\overrightarrow{OQ}=\overrightarrow{CO}$.
解答 解:设方格的边长为1,则:O(0,0),A((3,-3),B(1,-3),C(-2,3),
D(-2,2),P(-2,-2),Q(4,-1);
∴$\overrightarrow{OP}+\overrightarrow{OQ}=(2,-3)=\overrightarrow{CO}$.
故选C.
点评 考查向量坐标的概念,能确定图形上点的坐标,以及根据点的坐标求向量坐标,向量坐标的加法运算.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
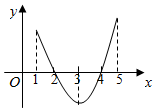 函数f(x)的定义域为R,它的导函数y=f′(x)的部分图象如图所示,则下面结论正确的是( )
函数f(x)的定义域为R,它的导函数y=f′(x)的部分图象如图所示,则下面结论正确的是( )| A. | 在(1,2)上函数f(x)为增函数 | |
| B. | 在(3,4)上函数f(x)为减函数 | |
| C. | 在(1,3)上函数f(x)有极大值 | |
| D. | x=3是函数f(x)在区间[1,5]上的极小值点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | ($\frac{1}{3}$,1) | C. | (0,$\frac{1}{3}$) | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 气温x (℃) | 18 | 13 | 10 | -1 |
| 山高y(km) | 24 | 34 | 38 | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l⊥m,m⊥n,则l∥n | B. | 若α⊥β,β⊥γ,则α∥γ | C. | 若α∥β,m⊥α,则m⊥β | D. | 若m∥α,m∥β,则α∥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com