解:(Ⅰ)令x
1=x
2=0,得f(x
0)=-f(0),①
令x
1=1,x
2=0,得f(x
0)=f(x
0)+f(1)+f(0),∴f(1)=-f(0)②
由①、②得f(x
0)=f(1),又因为f(x)为单调函数,∴x
0=1…(2分)
(Ⅱ)由(1)得f(x
1+x
2)=f(x
1)+f(x
2)+1,
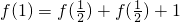
,∴
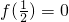
,a
1=1
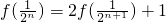
,…(3分)

…(4分)∴

,…(5分)
(Ⅲ)b
n=2lo

a
n+1=2n+1…(6分)
由{C
n}的构成法则可知,C
n应等于{b
n}中的n项之和,其第一项的项数为
[1+2+…+(n-1)]+1=
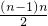
+1,即这一项为2×[
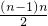
+1]-1=n(n-1)+1
C
n=n(n-1)+1+n(n-1)+3+…+n(n-1)+2n-1=n
2(n-1)+
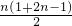
=n
3 …(8分)
1
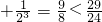
当n≥3时,
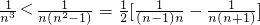
…(10分)
∴:
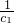
+
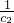
+
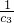
+…+
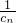
<

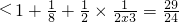
…(12分)
分析:(Ⅰ)分别令x
1=x
2=0,x
1=1,x
2=0,f(x
0)=f(1),又因为f(x)为单调函数,从而可求x
0的值;
(Ⅱ)由(1)得f(x
1+x
2)=f(x
1)+f(x
2)+1,进而可有
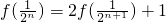
,从而有

,故可求;
(Ⅲ)先求得b
n=2n+1,由{C
n}的构成法则求得C
n=n
3 借助于当n≥3时,
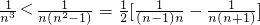
可进行放缩,从而得证.
点评:本题考查来哦赋值法,同时考查放缩法证明不等式,有一定的综合性.

 )+1,求{an}的通项公式;
)+1,求{an}的通项公式; an+1,将数列{bn}的项重新组合成新数列{cn},具体法则如下:c1=b1,c2=b2+b3,c3=b4+b5+b6,…,求证:
an+1,将数列{bn}的项重新组合成新数列{cn},具体法则如下:c1=b1,c2=b2+b3,c3=b4+b5+b6,…,求证: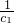 +
+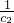 +
+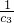 +…+
+…+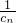 <
< .
.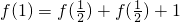 ,∴
,∴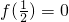 ,a1=1
,a1=1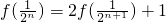 ,…(3分)
,…(3分) …(4分)∴
…(4分)∴ ,…(5分)
,…(5分) an+1=2n+1…(6分)
an+1=2n+1…(6分)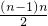 +1,即这一项为2×[
+1,即这一项为2×[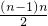 +1]-1=n(n-1)+1
+1]-1=n(n-1)+1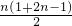 =n3 …(8分)
=n3 …(8分)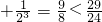
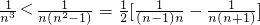 …(10分)
…(10分)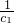 +
+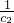 +
+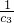 +…+
+…+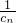 <
<
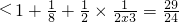
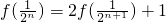 ,从而有
,从而有 ,故可求;
,故可求;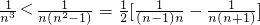 可进行放缩,从而得证.
可进行放缩,从而得证.

 全能练考卷系列答案
全能练考卷系列答案