
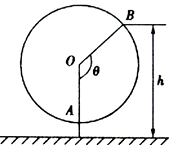
 如图是一个缆车示意图,该缆车的半径为4.8m,圆上最低点与地面的距离为0.8m,缆车每60s转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面的距离为hm.
如图是一个缆车示意图,该缆车的半径为4.8m,圆上最低点与地面的距离为0.8m,缆车每60s转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面的距离为hm.分析 (1)以圆心O为原点,以水平方向为x轴方向,以竖直方向为y轴方向建立平面直角坐标系,则根据缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,即可得到h与θ间的函数关系式;
(2)由60秒转动一圈,我们易得点A在圆上转动的角速度是$\frac{π}{30}$,故t秒转过的弧度数为$\frac{π}{30}$t,根据(1)的结论,我们将$\frac{π}{30}$t代入解析式,即可得到满足条件的t值.
解答 解:(1)以圆心O为原点,建立如图所示的平面直角坐标系,
则以Ox为始边,OB为终边的角为θ-$\frac{π}{2}$,
故点B的坐标为(4.8cos(θ-$\frac{π}{2}$),4.8sin(θ-$\frac{π}{2}$)),
∴h=5.6+4.8sin(θ-$\frac{π}{2}$)=5.6-4.8cosθ.
(2)点A在圆上转动的角速度是$\frac{π}{30}$,故t秒转过的弧度数为$\frac{π}{30}$t,
∴h=5.6-4.8cos$\frac{π}{30}$t,t∈[0,+∞).
当t=45s.h=5.6.
点评 本题考查的知识点是在实际问题中建立三角函数模型,在建立函数模型的过程中,以圆心O为原点,以水平方向为x轴方向,以竖直方向为Y轴方向建立平面直角坐标系,是解决本题的关键.综合性较强.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:选择题
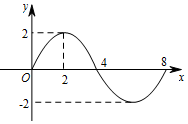 函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如示,则f(1)+f(2)+f(3)+…+f(210)的值等于( )
函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如示,则f(1)+f(2)+f(3)+…+f(210)的值等于( )| A. | $\sqrt{2}$ | B. | $2+2\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,+∞) | B. | [-4,+∞) | C. | (-3,+∞) | D. | [-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com