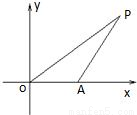
分析:先以O为原点,
所在直线为x轴建立直角坐标系,
||=c,P点坐标为(x
0,y
0),则
•
||•|y
0|=
×m×|y0|=m,即
|y0|=.因为
=(c,0),
=(x
0-c,y
0),
•
=1,可得
||=
=
,设
f(c)=c+,判断知f(c)在[2,+∞)上是增函数;所以当c=2时,f(c)为最小,从而
||为最小,此时P(
,),最终得到答案.
解答:解:
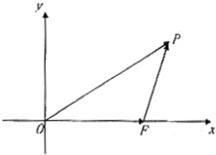
如图,以O为原点,
所在直线为x轴建立直角坐标系
设
||=c(c≥2),
S=c,
∴
•
||•|y
0|=
×m×|y0|=m,∴
|y0|=∵
=(c,0),
=(x
0-c,y
0),
•
=1
∴c(x
0-c)=1,∴
x0=c+∴
||=
=
设
f(c)=c+,当c≥2时,任取c
2>c
1≥2
有
f(c2)-f(c1)=c2+-c1-=(c2-c1)+=(c2-c1)(1-)当c
2>c
1≥2时,
<1,(1-)>0,c2-c1>0∴f(c
2)-f(c
1)>0,∴f(c)在[2,+∞)上是增函数
∴当c=2时,f(c)为最小,从而
||为最小,此时P(
,)
设椭圆的方程为
+=1(a>b>0),则
∴a
2=10,b
2=6
故椭圆的方程为
+=1.
故答案为:
+=1.
点评:本题主要考查向量的数量积运算和椭圆的标准方程的求法,解答的关键对向量的运算要相当熟悉,同时要善于利用函数思想求最值.

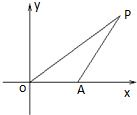 如图,已知△OAP的面积为S,
如图,已知△OAP的面积为S, 如图,以O为原点,
如图,以O为原点,

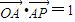 .设
.设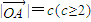 ,
,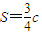 ,并且以O为中心、A为焦点的椭圆经过点P.当
,并且以O为中心、A为焦点的椭圆经过点P.当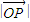 取得最小值时,则此椭圆的方程为 .
取得最小值时,则此椭圆的方程为 .