长方体ABCD-A1B1C1D1中,已知AB=a,BC=b,AA1=c,且a>b,求:
(1)下列异面直线之间的距离:AB与CC1;AB与A1C1;AB与B1C.
(2)异面直线D1B与AC所成角的余弦值.
分析:(1):主要是掌握异面直线距离的基本概念是两条直线的公垂线段,题中有的直接读出来(前两个有公垂线段),题中没有的话得先作出来再利用空间向量来求(第三个没有公垂线段);
(2)解法一连接转化:要求异面直线D1B与AC所成角的余弦值,先找异面直线D1B与AC所成角即找出连DD1的中点F,连接OF、AF,∠AOF就是异面直线D1B与AC所成的角.然后利用空间向量求角;
解法二利用添加法:在原长方体的右侧补上一个同样的长方体,连接BG、D1G,则AC∥BG,∴∠D1BG(或其补角)为D1B与AC所成的角.利用空间向量求角即可.
解答:(1)解:BC为异面直线AB与CC
1的公垂线段,故AB与CC
1的距离为b.
AA
1为异面直线AB与A
1C
1的公垂线段,故AB与A
1C
1的距离为c.
过B作BE⊥B
1C,垂足为E,则BE为异面直线AB与B
1C的公垂线,BE=
=
,即AB与B
1C的距离为
.
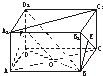
(2)解法一:连接BD交AC于点O,取DD
1的中点F,连接OF、AF,则OF∥D
1B,
∴∠AOF就是异面直线D
1B与AC所成的角.
∵AO=
,OF=
BD
1=
,AF=
,
∴在△AOF中,cos∠AOF═
.
解法二:如图,在原长方体的右侧补上一个同样的长方体,
连接BG、D
1G,则AC∥BG,∴∠D
1BG(或其补角)为D
1B与AC所成的角.
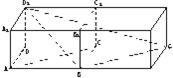
BD
1=
,BG=
,D
1G=
,
在△D
1BG中,cos∠D
1BG=
=-
,故所求的余弦值为
.
点评:此题考查学生空间想象能力以及对异面直线距离的理解,利用空间向量求出两直线间的距离和夹角.


 BD1=
BD1=

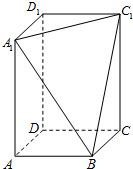 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.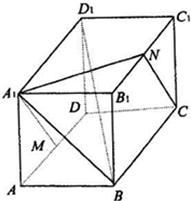 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC= 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点. 在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.