
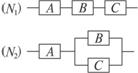
解析:分别记元件A、B、C正常工作为事件A、B、C,由已知条件P(A)=0.80,P(B)=0.90, P(C)=0.90.
(1)因为事件A、B、C是相互独立的,所以,系统N1正常工作的概率P1=P(A·B·C)=P(A)·P(B)·P(C)
=0.80×0.90×0.90=0.648.
故系统N1正常工作的概率为0.648.
(2)系统N2正常工作的概率
P2=P(A)·[1-P(![]() )]=P(A)[1-P(
)]=P(A)[1-P(![]() )·P(
)·P(![]() )].
)].
∵P(![]() )=1-P(B)=1-0.90=0.10,
)=1-P(B)=1-0.90=0.10,
P(![]() )=1-P(C)=1-0.90=0.10,
)=1-P(C)=1-0.90=0.10,
∴P2=0.80×(1-0.10×0.10)=0.80×0.99=0.792.
故系统N2正常工作的概率为0.792.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源:数学教研室 题型:044
查看答案和解析>>
科目:高中数学 来源:中华一题 高中数学必修3·B版(配套人民教育出版社实验教科书) 人教版 题型:044
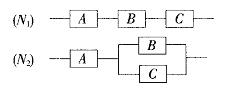
如图所示,用A、B、C三类不同的元件连接两个系统N1、N2,当元件A、B、C都正常工作时,系统N1正常工作;当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常工作.已知元件A、B、C正常工作的概率依次为0.80、0.90、0.90,分别求系统N1、N2正常工作的概率P1、P2.
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
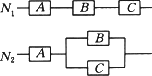
如图所示,用A、B、C三类不同的元件连接两个系统N1、N2,当元件A、B、C都正常工作时,系统N1正常工作;当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常工作,已知元素A、B、C正常工作的概率依次为0.80,0.90,0.90.分别求出系统N1、N2正常工作的概率P1、P2.
查看答案和解析>>
科目:高中数学 来源:高考零距离 二轮冲刺优化讲练 数学 题型:044
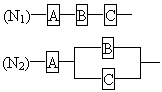
如图所示,用A、B、C三类不同的元件连接成两个系统N1、N2.当元件A、B、C都正常工作时,系统N1正常工作;当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常上作.
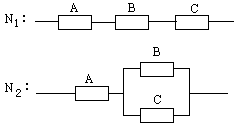
已知元件A、B、C正常T作的概率依次为0.80、0.90、0.90,分别求系统N1、N2正常工作的概率P1、P2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com