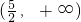定义在R上的函数f(x)为奇函数,且在[0,+∞)为增函数,对任意θ∈R,不等式f(cos2θ-3)+f(2m-sinθ)>0恒成立,则实数m的取值范围是 ________.
分析:本题是利用函数的单调性将抽象不等式变为三角不等式,再由三角函数的有界性求参数m的范围,本题中为了利用函数的单调性转化不等式需要根据函数的奇偶性将不等式f(cos2θ-3)+f(2m-sinθ)>0变为f(cos2θ-3)>f(-2m+sinθ),方便利用单调性转化.
解答:∵函数f(x)为奇函数且在[0,+∞)为增函数,易知函数f(x)为在(-∞,0]上递增,
∴函数f(x)在(-∞,+∞)上递增;
不等式f(cos2θ-3)+f(2m-sinθ)>0恒成立
?不等式f(cos2θ-3)>f(-2m+sinθ)恒成立
?不等式cos2θ-3>-2m+sinθ恒成立
?2m>2sin
2θ+sinθ+2恒成立,
记g(θ)=2sin
2θ+sinθ+2=2(sinθ+

)
2+

,
g(θ)
max=g(1)=5
∴2m>5?m>

.
故答案为
点评:本题考点是函数的奇偶性与单调性的综合,考查综合利用函数的奇偶性与单调性研究不等式恒成立时参数的取值范围,本题利用函数的性质将不等式恒成立求参数的问题转化为求函数最值的问题,本题中转化后求最值要注意三角函数的有界性,求解本题时两次利用转化的思想,第一次是将不等式转化为三角不等式,第二次是将三角不等式转化为求二次函数在某个区间上的最值,解题时要注意理解、领会本题中的转化策略及理论依据.

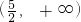
 )2+
)2+ ,
, .
.