
在实数范围内,不等式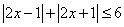 的解集为__________.
的解集为__________.
科目:高中数学 来源: 题型:
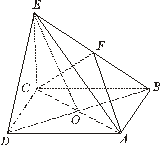
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
(Ⅰ) 求证:DE∥平面ACF;
(Ⅱ)若AB=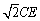 ,在线段EO上是否存在点G,使CG⊥平面BDE?若存在,求出
,在线段EO上是否存在点G,使CG⊥平面BDE?若存在,求出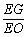 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
某创业投资公司拟投资开发某种新能源产品,估计能获得10万元到1000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金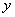 (单位:万元)随投资收益
(单位:万元)随投资收益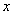 (单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)若建立函数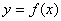 模型制定奖励方案,试用数学语言表述该公司对奖励函数
模型制定奖励方案,试用数学语言表述该公司对奖励函数
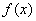 模型的基本要求,并分析函数
模型的基本要求,并分析函数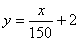 是否符合这个要求,并说明原因;
是否符合这个要求,并说明原因;
(2)若该公司采用函数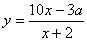 作为奖励函数模型,试确定最小的正整数
作为奖励函数模型,试确定最小的正整数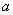 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数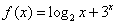 ,正实数
,正实数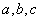 成公差为正数的等差数列,且满足
成公差为正数的等差数列,且满足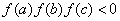 ,且实数
,且实数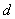 是函数
是函数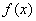 的一个零点。给出下列四个不等式:其中有可能成立的不等式有( )①
的一个零点。给出下列四个不等式:其中有可能成立的不等式有( )①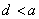 ;②
;②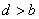 ;③
;③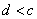 ;④
;④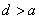 .
.
A ①②③④ B ②③④ C ①②③ D ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
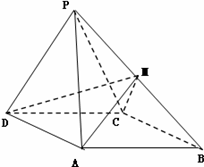
如图,四棱锥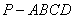 中,侧面
中,侧面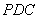 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面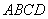 是
是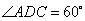 的菱形,
的菱形,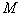 为
为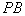 的中点.
的中点.
(Ⅰ)求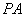 与底面
与底面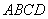 所成角的大小;
所成角的大小;
(Ⅱ)求证: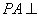 平面
平面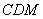 ;
;
(Ⅲ)求二面角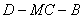 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知实数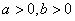 ,对于定义在
,对于定义在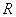 上的函数
上的函数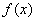 ,有下述命题:
,有下述命题:
①“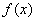 是奇函数”的充要条件是“函数
是奇函数”的充要条件是“函数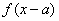 的图像关于点
的图像关于点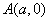 对称”;
对称”;
②“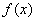 是偶函数”的充要条件是“函数
是偶函数”的充要条件是“函数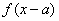 的图像关于直线
的图像关于直线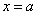 对称”;
对称”;
③“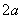 是
是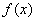 的一个周期”的充要条件是“对任意的
的一个周期”的充要条件是“对任意的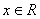 ,都有
,都有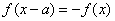 ”;
”;
④ “函数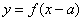 与
与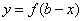 的图像关于
的图像关于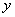 轴对称”的充要条件是“
轴对称”的充要条件是“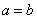 ”
”
其中正确命题的序号是
A.①② B.②③ C.①④ D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com