
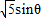 ,得到当θ=90°时,d最大,|MN|最短,再写出直线的方程.
,得到当θ=90°时,d最大,|MN|最短,再写出直线的方程.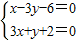 得A(0,-2)…(3分)
得A(0,-2)…(3分)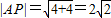
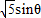
 ,
, (x-3)
(x-3)

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源:2012年普通高等学校招生全国统一考试浙江卷数学理科 题型:013
已知矩形ABCD,AB=1,BC=![]() .将△ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中,
.将△ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中,
A.存在某个位置,使得直线AC与直线BD垂直
B.存在某个位置,使得直线AB与直线CD垂直
C.存在某个位置,使得直线AD与直线BC垂直
D.对任意位置,三直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(浙江卷解析版) 题型:选择题
已知矩形ABCD,AB=1,BC=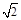 .将
.将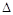 ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中,
ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中,
A.存在某个位置,使得直线AC与直线BD垂直
B.存在某个位置,使得直线AB与直线CD垂直
C.存在某个位置,使得直线AD与直线BC垂直
D.对任意位置,三直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省黄冈中学高一(下)期末数学试卷(理科)(解析版) 题型:选择题
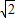 .将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( )
.将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( )查看答案和解析>>
科目:高中数学 来源:2012年浙江省高考数学试卷(理科)(解析版) 题型:选择题
 .将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( )
.将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com